Question

【題目】已知∠MON=90°，線段AB長為6cm，AB兩端分別在OM、ON上滑動，以AB為邊作正方形ABCD，對角線AC、BD相交于點P，連結OC．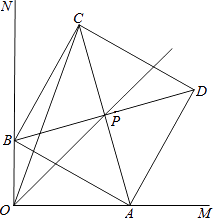

（1）求證：無論點A、點B怎樣運動，點P都在∠AOB的平分線上；
（2）若OP=4 ，求OA的長．
（3）求OC的最大值（提示：取AB的中點Q，連接CQ、OQ，運用兩點之間，線段最短）

Answer 1

【答案】
（1）

解：如圖，作PE⊥OM、PF⊥ON垂足分別為E、F，

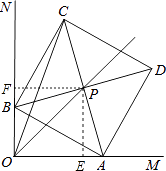
則∠PEA=∠PFB=90°=∠EOF，

∴∠EPF=90°，

∵ABCD是正方形，

∴PA=PB，且∠APB=90°，

∴∠APE+∠BPE=∠BPF+∠BPE，

即∠APE=∠BPF，

在△AEP和△BFP中，

，

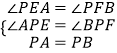∴△PAE≌△PBF（AAS），

∴PE=PF，

即點P在∠AOB的平分線上

（2）

解：∵四邊形OEPF是正方形，OP=4 ，

∴OE=PE=4，

又∵Rt△APB中，AB=6，

∴PA=3 ，

∴Rt△AEP中，AE= = ，

∴OA=OE+AE=4+ 或OA=OE﹣AE=4﹣

（3）

解：如圖，取AB的中點Q，連接OQ，CQ，OC，

∵AB長度不變，BC長度不變，

∴Rt△AOB中，OQ= AB=3，

Rt△BCQ中，CQ= =3 ，

∵OQ+CQ≥OC，

∴當O，C，Q三點共線時，OC有最大值，

OC最大值=OQ+QC=3+3 ．

【解析】（1）作PE⊥OM、PF⊥ON垂足分別為E、F，根據AAS判定△PAE≌△PBF，即可得出PE=PF，進而得到點P在∠AOB的平分線上；（2）根據四邊形OEPF是正方形，OP=4 ，可得OE=PE=4，再根據Rt△APB中，AB=6，可得PA=3 ，進而得到Rt△AEP中，AE= ，據此可得OA的長；（3）取AB的中點Q，連接OQ，CQ，OC，根據AB長度不變，BC長度不變，可得Rt△AOB中，OQ= AB=3，Rt△BCQ中，CQ=3 ，再根據OQ+CQ≥OC，可得當O，C，Q三點共線時，OC有最大值，進而得到OC最大值=OQ+QC=3+3 ．