
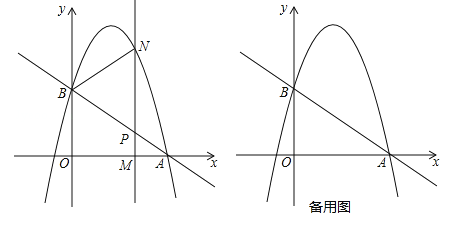
【題目】如圖,拋物線y=﹣![]() +bx+c過點A(3,0),B(0,2).M(m,0)為線段OA上一個動點(點M與點A不重合),過點M作垂直于x軸的直線與直線AB和拋物線分別交于點P、N.
+bx+c過點A(3,0),B(0,2).M(m,0)為線段OA上一個動點(點M與點A不重合),過點M作垂直于x軸的直線與直線AB和拋物線分別交于點P、N.
(1)求直線AB的解析式和拋物線的解析式;
(2)如果點P是MN的中點,那么求此時點N的坐標;
(3)在對稱軸的左側是否存在點M使四邊形OMPB的面積最大,如果存在求點M的坐標;不存在請說明理由.
【答案】(1)AB的解析式為y=﹣![]() x+2,拋物線解析式為y=﹣
x+2,拋物線解析式為y=﹣![]() x2+
x2+![]() x+2;(2)N點坐標為(
x+2;(2)N點坐標為(![]() );(3)不存在.
);(3)不存在.
【解析】試題分析:(1)用待定系數法分別求出直線AB的解析式和拋物線的解析式即可;(2)根據題意可得N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),即可得NP=﹣
m+2),即可得NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,再由NP=PM,可得方程﹣
m+2,再由NP=PM,可得方程﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解方程即可求得m的值,從而求得點N的坐標;(3)在對稱軸的左側不存在點M使四邊形OMPB的面積最大,根據題意和已知條件求出S梯形OMPB和m的函數關系式,利用二次函數的性質判定即可.
m+2,解方程即可求得m的值,從而求得點N的坐標;(3)在對稱軸的左側不存在點M使四邊形OMPB的面積最大,根據題意和已知條件求出S梯形OMPB和m的函數關系式,利用二次函數的性質判定即可.
試題解析:
(1)設直線AB的解析式為y=px+q,
把A(3,0),B(0,2)代入得![]() ,解得
,解得![]() ,
,
∴直線AB的解析式為y=﹣![]() x+2;
x+2;
把A(3,0),B(0,2)代入y=﹣![]() +bx+c得
+bx+c得 ,解得
,解得![]() ,
,
∴拋物線解析式為y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)∵M(m,0),MN⊥x軸,
∴N(m,﹣![]() m2+
m2+![]() m+2),P(m,﹣
m+2),P(m,﹣![]() m+2),
m+2),
∴NP=﹣![]() m2+4m,PM=﹣
m2+4m,PM=﹣![]() m+2,
m+2,
而NP=PM,
∴﹣![]() m2+4m=﹣
m2+4m=﹣![]() m+2,解得m1=3(舍去),m2=
m+2,解得m1=3(舍去),m2=![]() ,
,
∴N點坐標為(![]() ,
,![]() );
);
(3)在對稱軸的左側不存在點M使四邊形OMPB的面積最大,理由如下:
B(0,2),M(m,0),MN⊥x軸,
∴P(m,﹣![]() m+2),
m+2),
S梯形OMPB=![]() (PM+OB)OM=
(PM+OB)OM=![]() (﹣
(﹣![]() m+2+2)m
m+2+2)m
=﹣![]() m2+2m
m2+2m
=﹣![]() (m﹣3)2+3
(m﹣3)2+3
∵對稱軸是x=﹣![]() =
=![]() ,M在對稱軸的左側,
,M在對稱軸的左側,
∴0<m<![]() ,
,
∴m的值無法確定,
在對稱軸的左側不存在點M使四邊形OMPB的面積最大.


 小學教材全測系列答案
小學教材全測系列答案 小學數學口算題卡脫口而出系列答案
小學數學口算題卡脫口而出系列答案 優秀生應用題卡口算天天練系列答案
優秀生應用題卡口算天天練系列答案 浙江之星課時優化作業系列答案
浙江之星課時優化作業系列答案科目:初中數學 來源: 題型:
【題目】下列四幅圖象近似刻畫兩個變量之間的關系,請按圖象順序將下面四種情景與之對應排序( ).
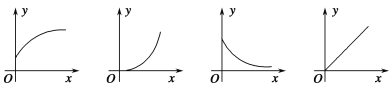
①一輛汽車在公路上勻速行駛(汽車行駛的路程與時間的關系)
②向錐形瓶中勻速注水(水面的高度與注水時間的關系)
③將常溫下的溫度計插入一杯熱水中(溫度計的讀數與時間的關系)
④一杯越來越涼的水(水溫與時間的關系)
A.①②④③ B.③④②①
C.①④②③ D.③②④①
查看答案和解析>>
科目:初中數學 來源: 題型:
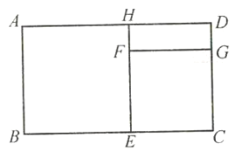
【題目】如圖,長方形![]() 中,長
中,長![]() ,寬
,寬![]() ,四邊形
,四邊形![]() 和四邊形
和四邊形![]() 都是正方形.
都是正方形.
(1)求四邊形![]() 的面積(用含
的面積(用含![]() 、
、![]() 的代數式表示);
的代數式表示);
(2)當![]() 、
、![]() 滿足什么等量關系時,圖形是一個軸對稱圖形.
滿足什么等量關系時,圖形是一個軸對稱圖形.
查看答案和解析>>
科目:初中數學 來源: 題型:
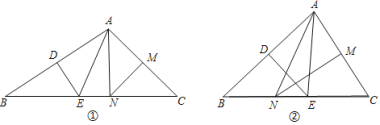
【題目】已知等邊△ABC的邊長為![]() ,D是AB上的動點,過D作DE⊥AC于點E,過E作EF⊥BC于點F,過F作FG⊥AB于點G.當G與D重合時,AD的長是( )
,D是AB上的動點,過D作DE⊥AC于點E,過E作EF⊥BC于點F,過F作FG⊥AB于點G.當G與D重合時,AD的長是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某體育用品商場預測某品牌運動服能夠暢銷,就用32000元購進了一批這種運動服,上市后很快脫銷,商場又用68000元購進第二批這種運動服,所購數量是第一批購進數量的2倍,但每套進價多了10元.
(1)該商場兩次共購進這種運動服多少套?
(2)如果這兩批運動服每套的售價相同,且全部售完后總利潤不低于20%,那么每套售價至少是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() 垂直平分
垂直平分![]() ,分別交
,分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,
,![]() 垂直平分
垂直平分![]() ,分別交
,分別交![]() ,
,![]() 于點
于點![]() 、
、![]() .
.
⑴如圖①,若![]() ,求
,求![]() 的度數;
的度數;
⑵如圖②,若![]() ,求
,求![]() 的度數;
的度數;
⑶若![]()
![]() ,直接寫出用
,直接寫出用![]() 表示
表示![]() 大小的代數式.
大小的代數式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有一個種植總面積為![]() 的矩形塑料溫棚,分壟間隔套種草莓和西紅柿共
的矩形塑料溫棚,分壟間隔套種草莓和西紅柿共![]() 壟,種植的草莓或西紅柿單種農作物的總壟數不低于8壟,又不超過
壟,種植的草莓或西紅柿單種農作物的總壟數不低于8壟,又不超過![]() 壟(壟數為正整數),它們的占地面積、產量、利潤分別如下:
壟(壟數為正整數),它們的占地面積、產量、利潤分別如下:
⑴若設草莓共種植了![]() 壟,通過計算說明共有幾種種植方案?分別是哪幾種?
壟,通過計算說明共有幾種種植方案?分別是哪幾種?
⑵在這幾種種植方案中,哪種方案獲得的利潤最大?最大利潤是多少?
占地面積(m2/壟) | 產量(千克/壟) | 利潤(元/千克) | |
西紅柿 | 32 | 160 | 1.0 |
草莓 | 15 | 50 | 1.6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,點E,F分別在邊AB與CD上,點G、H在對角線AC上,AG=CH,BE=DF.
(1)求證:四邊形EGFH是平行四邊形;
(2)若EG=EH,AB=8,BC=4.求AE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明最喜歡吃芝麻餡的湯圓了,一天早晨小明媽媽給小明下了四個大湯圓,一個花生餡,一個水果餡,兩個芝麻餡,四個湯圓除內部餡料不同外,其他一切均相同.
(1)求小明吃第一個湯圓恰好是芝麻餡的概率;
(2)請利用樹狀圖或列表法,求小明吃前兩個湯圓恰好是芝麻餡的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com