
【題目】三角板ABC中,∠ACB=90°,∠B=30°,AC=2 ![]() ,三角板繞直角頂點C逆時針旋轉,當點A的對應點A′落在AB邊的起始位置上時即停止轉動,則B點轉過的路徑長為( )
,三角板繞直角頂點C逆時針旋轉,當點A的對應點A′落在AB邊的起始位置上時即停止轉動,則B點轉過的路徑長為( ) 
A.![]() π
π
B.![]() π
π
C.2π
D.3π
【答案】C
【解析】解:∵∠B=30°,AC=2 ![]() ,
,
∴BA=4 ![]() ,∠A=60°,
,∠A=60°,
∴CB=6,
∵AC=A′C,
∴∠AA′C是等邊三角形,
∴∠ACA′=60°,
∴∠BCB′=60°,
∴弧長l= ![]() =
= ![]() =2π,
=2π,
故選C.
【考點精析】解答此題的關鍵在于理解弧長計算公式的相關知識,掌握若設⊙O半徑為R,n°的圓心角所對的弧長為l,則l=nπr/180;注意:在應用弧長公式進行計算時,要注意公式中n的意義.n表示1°圓心角的倍數,它是不帶單位的,以及對旋轉的性質的理解,了解①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】某校實行學案式教學,需印制若干份教學學案.印刷廠有,甲、乙兩種收費方式,除按印數收取印刷費外,甲種方式還需收取制版費而乙種不需要,兩種印刷方式的費用y(元)與印刷份數x(份)之間的關系如圖所示.
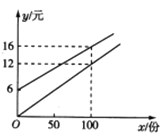
(1)填空:甲種收費方式的函數關系式是__________,乙種收費方式的函數關系式是__________.
(2)該校某年級每次需印制100~450(含100和450)份學案,選擇哪種印刷方式較合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
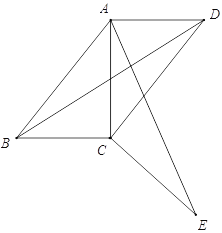
【題目】如圖,四邊形ABCD中,∠ABC=∠ADC=45°,將△BCD繞點C順時針旋轉一定角度后,點B的對應點恰好與點A重合,得到△ACE.
(1)求證:AE⊥BD;
(2)若AD=2,CD=3,試求出四邊形ABCD的對角線BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標分別為A(1,1),B(4,2),C(3,4).
(1) 請畫出△ABC向左平移5個單位長度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 請畫出△ABC關于原點對稱的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.
軸上求作一點P,使△PAB的周長最小,請畫出△PAB,并直接寫出P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+c與x軸交于A,B兩點,頂點為C,點P為拋物線上,且位于x軸下方.
(1)如圖1,若P(1,﹣3),B(4,0).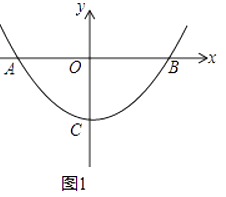
①求該拋物線的解析式;
②若D是拋物線上一點,滿足∠DPO=∠POB,求點D的坐標;
(2)如圖2,已知直線PA,PB與y軸分別交于E、F兩點.當點P運動時, ![]() 是否為定值?若是,試求出該定值;若不是,請說明理由.
是否為定值?若是,試求出該定值;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將△ABC紙片沿DE折疊,使點A落在點A'處,且A'B平分∠ABC,A'C平分∠ACB,若∠BA'C=110°,則∠1+∠2的度數為( )

A. 80°; B. 90°; C. 100°; D. 110°;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請你用學習“一次函數”時積累的經驗和方法研究函數y=|x|的圖象和性質,并解決問題.
(1)完成下列步驟,畫出函數y=|x|的圖象;
①列表、填空;
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | 3 | 1 | 1 | 2 | 3 | … |
②描點;
③連線.
(2)觀察圖象,當x 時,y隨x的增大而增大;
(3)根據圖象,不等式|x|<![]() x+
x+![]() 的解集為 .
的解集為 .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形ABCD的邊長為2cm,∠DAB=60°.點P從A點出發,以 ![]() cm/s的速度,沿AC向C作勻速運動;與此同時,點Q也從A點出發,以1cm/s的速度,沿射線AB作勻速運動.當P運動到C點時,P、Q都停止運動.設點P運動的時間為ts.
cm/s的速度,沿AC向C作勻速運動;與此同時,點Q也從A點出發,以1cm/s的速度,沿射線AB作勻速運動.當P運動到C點時,P、Q都停止運動.設點P運動的時間為ts. 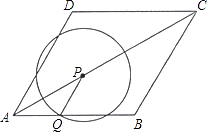
(1)當P異于A、C時,請說明PQ∥BC;
(2)以P為圓心、PQ長為半徑作圓,請問:在整個運動過程中,t為怎樣的值時,⊙P與邊BC分別有1個公共點和2個公共點?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】目前節能燈在城市已基本普及,今年山東省面向縣級及農村地區推廣,為響應號召,某商場計劃購進甲,乙兩種節能燈共1200只,這兩種節能燈的進價、售價如下表:
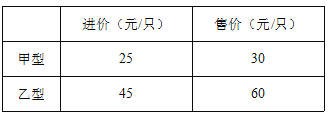
(1)如何進貨,進貨款恰好為46000元?
(2)設商場購進甲種節能燈x只,求出商場銷售完節能燈時總利潤w與購進甲種節能燈x之間的函數關系式;
(3)如何進貨,商場銷售完節能燈時獲利最多且不超過進貨價的30%,此時利潤為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com