
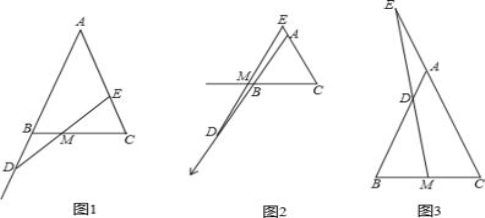
已知在等腰△ABC中,AB=AC,在射線CA上截取線段CE,在射線AB上截取線段BD,連接DE,DE所在直線交直線BC與點M。請探究:
(1)如圖(1),當點E在線段AC上,點D在AB延長線上時,若BD=CE,請判斷線段MD和線段ME的數量關系,并證明你的結論。
(2)如圖(2),當點E在CA的延長線上,點D在AB的延長線上時,若BD=CE,則(1)中的結論還成立嗎?如果成立,請證明;如果不成立,說明理由;
(3)如圖(3),當點E在CA的延長線上,點D在線段AB上(點D不與A,B重合),DE所在直線與直線BC交于點M,若CE=2BD,請直接寫出線段MD與線段ME的數量關系。
(1)DM=EM.理由見解析;(2)成立,理由見解析;(3)MD=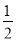 ME.
ME.
【解析】
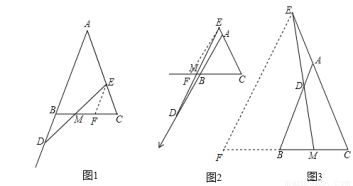
試題分析:(1)DM=EM;過點E作EF∥AB交BC于點F,然后利用平行線的性質和已知條件可以證明△DBM≌△EFM,接著利用全等三角形的性質即可證明題目的結論;
(2)成立;過點E作EF∥AB交CB的延長線于點F,然后利用平行線的性質與已知條件可以證明△DBM≌△EFM,接著利用全等三角形的性質即可證明題目的結論;
(3)MD=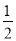 ME.過點E作EF∥AB交CB的延長線于點F,然后利用平行線的性質和已知條件得到△DBM∽△EFM,接著利用相似三角形的性質即可得到結論;
ME.過點E作EF∥AB交CB的延長線于點F,然后利用平行線的性質和已知條件得到△DBM∽△EFM,接著利用相似三角形的性質即可得到結論;
試題解析:(1)DM=EM;(1分)
證明:過點E作EF∥AB交BC于點F,(2分)
∵AB=AC,
∴∠ABC=∠C;
又∵EF∥AB,
∴∠ABC=∠EFC,
∴∠EFC=∠C,
∴EF=EC.
又∵BD=EC,
∴EF=BD.
又∵EF∥AB,
∴∠ADM=∠MEF.
在△DBM和△EFM中
 ,
,
∴△DBM≌△EFM,
∴DM=EM.
(2)成立;
證明:過點E作EF∥AB交CB的延長線于點F,
∵AB=AC,
∴∠ABC=∠C;
又∵EF∥AB,
∴∠ABC=∠EFC,
∴∠EFC=∠C,
∴EF=EC.
又∵BD=EC,
∴EF=BD.
又∵EF∥AB,
∴∠ADM=∠MEF.
在△DBM和△EFM中

∴△DBM≌△EFM;
∴DM=EM;
(3)過點E作EF∥AB交CB的延長線于點F,
∴△DBM∽△EFM,
∴BD:EF=DM:ME,
∵AB=AC,
∴∠ABC=∠C,
∵∠F=∠ABC,
∴∠F=∠C,
∴EF=EC,
∴BD:EC=DM:ME=1:2,
∴MD=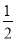 ME.
ME.
考點:全等三角形的判定與性質.


科目:初中數學 來源:2014-2015學年河北省沙河市九年級上學期第二次模擬數學試卷(解析版) 題型:選擇題
下列方程是一元 二次方程的是 ( )
A.x+2y=1 B.x=2x3-3 C x2-2=0 D 
查看答案和解析>>
科目:初中數學 來源:2014-2015學年安徽省宣城市涇縣琴溪片九年級上學期期中聯考數學試卷(解析版) 題型:選擇題
反比例函數y= 的圖象,在每個象限內,y的值隨x值的增大而增大,則k可以為( )
的圖象,在每個象限內,y的值隨x值的增大而增大,則k可以為( )
A、0 B、1 C、2 D、3
查看答案和解析>>
科目:初中數學 來源:2014-2015學年天津寶坻王卜莊鎮初中八年級上學期期中考試數學試卷(解析版) 題型:填空題
等腰三角形的周長為20cm,一邊長為6cm,則底邊長為______.
查看答案和解析>>
科目:初中數學 來源:2014-2015學年天津寶坻王卜莊鎮初中八年級上學期期中考試數學試卷(解析版) 題型:選擇題
如圖所示,AB∥CD,∠A=45°,∠C=29°,則∠E的度數為( )
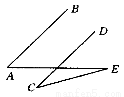
A.22.5° B.16° C.18° D.29°
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇東臺蘇東雙語八年級上學期第一次質檢數學試卷(解析版) 題型:解答題
如圖,鐵路上A,B兩點相距25km,C,D為兩村莊,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,現在要在鐵路AB上建一個土特產品收購站E,使得C,D兩村到E站的距離相等,則E站應建在離A站多少km處?

查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇東臺蘇東雙語八年級上學期第一次質檢數學試卷(解析版) 題型:填空題
已知┃x-12┃+┃z-13┃與y2-10y+25互為相反數,則以x、y、z為三邊的三角形是 三角形。
查看答案和解析>>
科目:初中數學 來源:2014-2015學年江蘇啟東南苑中學七年級上學期第一單元測試數學試卷(解析版) 題型:解答題
對于自然數a、b、c、d,定義
 表示運算ac-bd.
表示運算ac-bd.
(1) 求
 的值;
的值;
(2) 已知
 =2,求bd的值.
=2,求bd的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com