
【題目】如圖,Rt△ABC中,∠ACB=90°,AC=BC,D是線段AB上一點(0<AD<![]() AB).過點B作BE⊥CD,垂足為E.將線段CE繞點C逆時針旋轉90°,得到線段CF,連接AF,EF.設∠BCE的度數為α.
AB).過點B作BE⊥CD,垂足為E.將線段CE繞點C逆時針旋轉90°,得到線段CF,連接AF,EF.設∠BCE的度數為α.
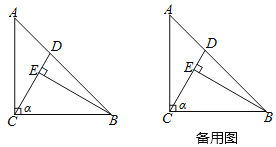
(1)①依題意補全圖形.
②若α=60°,則∠CAF=_____°;![]() =_____;
=_____;
(2)用含α的式子表示EF與AB之間的數量關系,并證明.
【答案】(1)①補圖見解析;②30,![]() ;(2)EF=ABcosα;證明見解析.
;(2)EF=ABcosα;證明見解析.
【解析】
(1)①利用旋轉直接畫出圖形,
②先求出∠CBE=30°,再判斷出△ACF≌△BCE,得出∠CAF=30°,再利用等腰直角三角形的性質計算即可得出結論;
(2)先判斷出△ACF≌△BCE,得出∠CAF=α,再同(1)②的方法即可得出結論.
(1)①將線段CE繞點C逆時針旋轉90°,得到線段CF,連接AF,EF,如圖1;
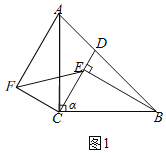
②∵BE⊥CD,∠CEB=90°,
∵α=60°,
∴∠CBE=30°,
在Rt△ABC中,AC=BC,
∴AC=![]() AB,
AB,
∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
在△ACF和△BCE中,
AC=BC,∠FCA=∠ECB,FC=EC,
∴△ACF≌△BCE(SAS),
∴∠AFC=∠BEC=90°,∠CAF=∠CBE=30°,
∴CF=![]() AC,
AC,
由旋轉知,CF=CE,∠ECF=90°,
∴EF=![]() CF=
CF=![]() AC=
AC=![]() ×
×![]() AB=
AB=![]() AB,
AB,
∴![]() =
=![]() ,
,
故答案為30,![]() ;
;
(2)EF=ABcosα.
證明:∵∠FCA=90°﹣∠ACE,∠ECB=90°﹣∠ACE,
∴∠FCA=∠ECB=α.
同(1)②的方法知,△ACF≌△BCE,
∴∠AFC=∠BEC=90°,
∴在Rt△AFC中,cos∠FCA=![]() .
.
∵∠ACB=90°,AC=BC,
∴∠CAB=∠CBA=45°.
∵∠ECF=90°,CE=CF,
∴∠CFE=∠CEF=45°.
在△FCE和△ACB中,
∠FCE=∠ACB=90°,
∠CFE=∠CAB=45°,
∴△FCE∽△ACB,
∴![]() =cos∠FCA=cosα,
=cos∠FCA=cosα,
即EF=ABcosα.


科目:初中數學 來源: 題型:
【題目】在直角坐標系![]() 中,
中,![]() 、
、![]() ,將
,將![]() 經過旋轉、平移變化后得到如圖1所示的
經過旋轉、平移變化后得到如圖1所示的![]() .
.
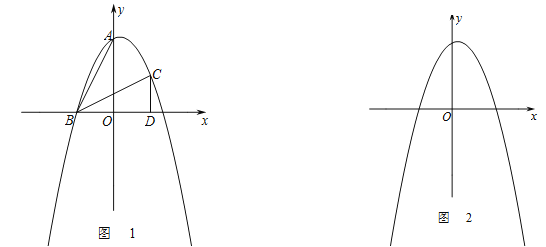
(1)求經過![]() 、
、![]() 、
、![]() 三點的拋物線的解析式;
三點的拋物線的解析式;
(2)連結![]() ,點
,點![]() 是位于線段
是位于線段![]() 上方的拋物線上一動點,若直線
上方的拋物線上一動點,若直線![]() 將
將![]() 的面積分成
的面積分成![]() 兩部分,求此時點
兩部分,求此時點![]() 的坐標;
的坐標;
(3)現將![]() 、
、![]() 分別向下、向左以
分別向下、向左以![]() 的速度同時平移,求出在此運動過程中
的速度同時平移,求出在此運動過程中![]() 與
與![]() 重疊部分面積的最大值.
重疊部分面積的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
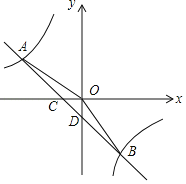
【題目】如圖,在平面直角坐標系中,一次函數y=ax+b的圖象與反比例函數y=![]() 的圖象交于第二、四象限內的A,B兩點,與x軸交于點C,與y軸交于點D,點B的坐標是(m,﹣4),連接AO,AO=5,sin∠AOC=
的圖象交于第二、四象限內的A,B兩點,與x軸交于點C,與y軸交于點D,點B的坐標是(m,﹣4),連接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函數和一次函數的解析式;
(2)連接OB,求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖1是一輛登高云梯消防車的實物圖,圖2是其工作示意圖,起重臂AC是可伸縮的,其轉動點A距離地面BD的高度AE為3.5m.當AC長度為9m,張角∠CAE為112°時,求云梯消防車最高點C距離地面的高度CF.(結果精確到0.1m,參考數據:sin22°≈0.37,cos22°≈0.93,tan22°≈0.40.)
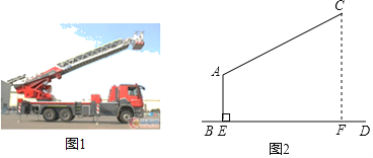
查看答案和解析>>
科目:初中數學 來源: 題型:
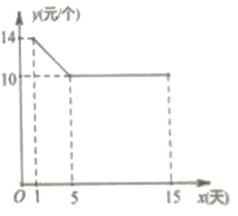
【題目】每年九月開學前后是文具盒的銷售旺季,商場專門設置了文具盒專柜李經理記錄了![]() 天的銷售數量和銷售單價,其中銷售單價
天的銷售數量和銷售單價,其中銷售單價![]() (元/個)與時間第
(元/個)與時間第![]() 天(
天(![]() 為整數)的數量關系如圖所示,日銷量
為整數)的數量關系如圖所示,日銷量![]() (個)與時間第
(個)與時間第![]() 天(
天(![]() 為整數)的函數關系式為:
為整數)的函數關系式為: 
![]() 直接寫出
直接寫出![]() 與
與![]() 的函數關系式,并注明自變量
的函數關系式,并注明自變量![]() 的取值范圍;
的取值范圍;
![]() 設日銷售額為
設日銷售額為![]() (元) ,求
(元) ,求![]() (元)關于
(元)關于![]() (天)的函數解析式;在這
(天)的函數解析式;在這![]() 天中,哪一天銷售額
天中,哪一天銷售額![]() (元)達到最大,最大銷售額是多少元;
(元)達到最大,最大銷售額是多少元;
![]() 由于需要進貨成本和人員工資等各種開支,如果每天的營業額低于
由于需要進貨成本和人員工資等各種開支,如果每天的營業額低于![]() 元,文具盒專柜將虧損,直接寫出哪幾天文具盒專柜處于虧損狀態
元,文具盒專柜將虧損,直接寫出哪幾天文具盒專柜處于虧損狀態
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為積極響應新舊動能轉換.提高公司經濟效益.某科技公司近期研發出一種新型高科技設備,每臺設備成本價為30萬元,經過市場調研發現,每臺售價為40萬元時,年銷售量為600臺;每臺售價為45萬元時,年銷售量為550臺.假定該設備的年銷售量y(單位:臺)和銷售單價![]() (單位:萬元)成一次函數關系.
(單位:萬元)成一次函數關系.
(1)求年銷售量![]() 與銷售單價
與銷售單價![]() 的函數關系式;
的函數關系式;
(2)根據相關規定,此設備的銷售單價不得高于70萬元,如果該公司想獲得10000萬元的年利潤.則該設備的銷售單價應是多少萬元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com