
【題目】如圖,水平放置的圓柱形排水管的截面為⊙O,有水部分弓形的高為2,弦AB=4 ![]() ,求⊙O的半徑.
,求⊙O的半徑.
【答案】解:過點O作OC⊥AB于點C,交 ![]() 于點D,連接OB,
于點D,連接OB, 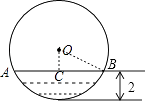
設⊙O的半徑為r,則OC=r﹣2,
∵OC⊥AB,
∴BC= ![]() AB=
AB= ![]() ×4
×4 ![]() =2
=2 ![]() ,
,
在Rt△BOC中,
∵OC2+BC2=OB2,即(r﹣2)2+(2 ![]() )2=r2,
)2=r2,
解得r=4.
【解析】此類問題通過添加輔助線過點O作OC⊥AB于點C,交弧AB于點D,連接OB,根據垂徑定理求出BC的長,再用含r的代數式表示出OC的長,然后根據勾股定理建立方程求解即可。
【考點精析】通過靈活運用勾股定理的概念和垂徑定理,掌握直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2;垂徑定理:平分弦(不是直徑)的直徑垂直于弦,并且平分弦所對的兩條弧即可以解答此題.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知數軸上點![]() 表示的數為
表示的數為![]() ,
,![]() 是數軸上位于點
是數軸上位于點![]() 左側一點,且AB=20,動點
左側一點,且AB=20,動點![]() 從
從![]() 點出發,以每秒
點出發,以每秒![]() 個單位長度的速度沿數軸向左勻速運動,設運動時間t(t>0)秒.
個單位長度的速度沿數軸向左勻速運動,設運動時間t(t>0)秒.
![]()
(1)寫出數軸上點![]() 表示的數______;點
表示的數______;點![]() 表示的數_______(用含
表示的數_______(用含![]() 的代數式表示)
的代數式表示)
(2)動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿數軸向右勻速運動,若點
個單位長度的速度沿數軸向右勻速運動,若點![]() 、
、![]() 同時出發,問多少秒時
同時出發,問多少秒時![]() 、
、![]() 之間的距離恰好等于
之間的距離恰好等于![]() ?
?
(3)動點![]() 從點
從點![]() 出發,以每秒
出發,以每秒![]() 個單位長度的速度沿數軸向左勻速運動,若點
個單位長度的速度沿數軸向左勻速運動,若點![]() 、
、![]() 同時出發,問多少秒時
同時出發,問多少秒時![]() 、
、![]() span>之間的距離恰好又等于
span>之間的距離恰好又等于![]() ?
?
(4)若![]() 為
為![]() 的中點,
的中點,![]() 為
為![]() 的中點,在點
的中點,在點![]() 運動的過程中,線段
運動的過程中,線段![]() 的長度是否發生變化?若變化,請說明理由,若不變,請畫出圖形,并求出線段
的長度是否發生變化?若變化,請說明理由,若不變,請畫出圖形,并求出線段![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一次函數y=﹣x+5的圖象與反比例函數y= ![]() (k≠0)在第一象限的圖象交于A(1,n)和B兩點.
(k≠0)在第一象限的圖象交于A(1,n)和B兩點.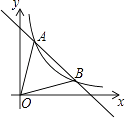
(1)求反比例函數的解析式與點B坐標;
(2)求△AOB的面積;
(3)在第一象限內,當一次函數y=﹣x+5的值小于反比例函數y= ![]() (k≠0)的值時,寫出自變量x的取值范圍.
(k≠0)的值時,寫出自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著“互聯網+”時代的到來,一種新型打車方式受到大眾歡迎,該打車方式的總費用由里程費和耗時費組成,其中里程費按x元/公里計算,耗時費按y元/分鐘計算(總費用不足9元按9元計價).小明、小剛兩人用該打車方式出行,按上述計價規則,其打車總費用、行駛里程數與打車時間如表:
時間(分鐘) | 里程數(公里) | 車費(元) | |
小明 | 8 | 8 | 12 |
小剛 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小華也用該打車方式,打車行駛了11公里,用了14分鐘,那么小華的打車總費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等邊三角形ABC中,點E在AB上,點D在CB的延長線上,且ED=EC.
(1)(觀察猜想)當點E在AB的中點時,如圖1,過點E作EF∥BC,交AC于點F,觀察猜想得到線段AE與DB的大小關系是 ;
(2)(探究證明)當點E不是AB的中點時,如圖2,上述結論是否成立,如果成立,請寫出解答過程,如果不成立,請說明理由;
(3)(拓展延伸)在等邊三角形ABC中,點E在直線AB上,點D在直線BC上,且ED=EC,若△ABC的邊長為2,AE=1,求CD的長(請直接寫出結果).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,過點A1(1,0)作x軸的垂線,交直線y=2x于點B1;點A2與點O關于直線A1B1對稱;過點A2(2,0)作x軸的垂線,交直線y=2x于點B2;點A3與點O關于直線A2B2對稱;過點A3(4,0)作x軸的垂線,交直線y=2x于點B3;…,按此規律作下去,則點Bn的坐標為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象經過點(﹣1,4),且與直線y=﹣ ![]() x+1相交于A、B兩點(如圖),A點在y軸上,過點B作BC⊥x軸,垂足為點C(﹣3,0).
x+1相交于A、B兩點(如圖),A點在y軸上,過點B作BC⊥x軸,垂足為點C(﹣3,0).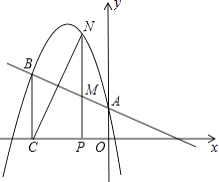
(1)求二次函數的表達式;
(2)點N是二次函數圖象上一點(點N在AB上方),過N作NP⊥x軸,垂足為點P,交AB于點M,求MN的最大值;
(3)在(2)的條件下,點N在何位置時,BM與NC相互垂直平分?并求出所有滿足條件的N點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一項工程,甲隊單獨做需40天完成,若乙隊先做30天后,甲、乙兩隊一起合做20天恰好完成任務,請問:
(1)乙隊單獨做需要多少天才能完成任務?
(2)現將該工程分成兩部分,甲隊做其中一部分工程用了x天,乙隊做另一部分工程用了y天,若x; y都是正整數,且甲隊做的時間不到15天,乙隊做的時間不到70天,那么兩隊實際各做了多少天?
查看答案和解析>>
科目:初中數學 來源: 題型:
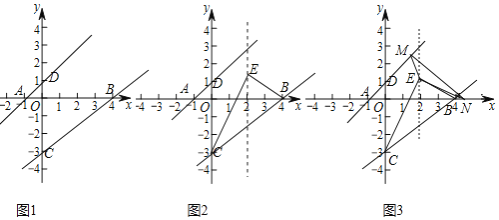
【題目】如圖1,點A、B、C在坐標軸上,且A、B、C的坐標分別為![]() 、
、![]() 、
、![]() 過點A的直線AD與y軸正半軸交于點D,
過點A的直線AD與y軸正半軸交于點D,![]()
![]() 求直線AD和BC的解析式;
求直線AD和BC的解析式;
![]() 如圖2,點E在直線
如圖2,點E在直線![]() 上且在直線BC上方,當
上且在直線BC上方,當![]() 的面積為6時,求E點坐標;
的面積為6時,求E點坐標;
![]() 在
在![]() 的條件下,如圖3,動點M在直線AD上,動點N在x軸上,連接ME、NE、MN,當
的條件下,如圖3,動點M在直線AD上,動點N在x軸上,連接ME、NE、MN,當![]() 周長最小時,求
周長最小時,求![]() 周長的最小值.
周長的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com