
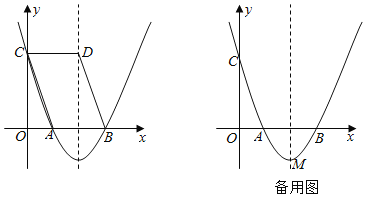
【題目】如圖,已知二次函數(shù)y=ax2﹣8ax+6(a>0)的圖象與x軸分別交于A、B兩點,與y軸交于點C,點D在拋物線的對稱軸上,且四邊形ABDC為平行四邊形.
(1)求此拋物線的對稱軸,并確定此二次函數(shù)的表達式;
(2)點E為x軸下方拋物線上一點,若△ODE的面積為12,求點E的坐標(biāo);
(3)在(2)的條件下,設(shè)拋物線的頂點為M,點P是拋物線的對稱軸上一動點,連接PE、EM,過點P作PE的垂線交拋物線于點Q,當(dāng)∠PQE=∠EMP時,求點Q到拋物線的對稱軸的距離.
【答案】(1)x=4,y=![]() x2﹣4x+6;(2)(3,-
x2﹣4x+6;(2)(3,-![]() );(3)4或2+
);(3)4或2+![]()
【解析】
(1)先求出對稱軸為x=4,進而求出AB=4,進而求出點A,B坐標(biāo),即可得出結(jié)論;
(2)根據(jù)E點在拋物線y=![]() x2﹣4x+6上,設(shè)E(m,
x2﹣4x+6上,設(shè)E(m,![]() m2﹣4m+6),作EN⊥y軸于N,利用面積的和差:S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE建立方程求解,即可得出結(jié)論;
m2﹣4m+6),作EN⊥y軸于N,利用面積的和差:S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE建立方程求解,即可得出結(jié)論;
(3)①當(dāng)點Q在對稱軸右側(cè)時,先判斷出點E,M,Q,P四點共圓,得出∠EMQ=90°,利用同角的余角相等判斷出∠EMF=∠HGM,得出tan∠EMF=![]() =2,得出HG=
=2,得出HG=![]() HM=1,進而求出Q(8,6),得出結(jié)論;
HM=1,進而求出Q(8,6),得出結(jié)論;
②當(dāng)點Q在對稱軸左側(cè)時,先判斷出△PDQ∽△EFP,得出![]() ,進而判斷出DP=
,進而判斷出DP=![]() ,PF=2QD,即可得出結(jié)論.
,PF=2QD,即可得出結(jié)論.
解:(1)對稱軸為直線x=﹣![]() ,則CD=4,
,則CD=4,
∵四邊形ABDC為平行四邊形,
∴DC∥AB,DC=AB,
∴DC=AB=4,
∴A(2,0),B(6,0),
把點 A(2,0)代入得y=ax2﹣8ax+12得4a﹣16a+6=0,解得a=![]() ,
,
∴二次函數(shù)解析式為y=![]() x2﹣4x+6;
x2﹣4x+6;
(2)如圖1,設(shè)E(m,![]() m2﹣4m+6),其中2<m<6,作EN⊥y軸于N,
m2﹣4m+6),其中2<m<6,作EN⊥y軸于N,
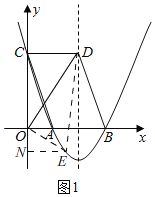
∵S梯形CDEN﹣S△OCD﹣S△OEN=S△ODE,
∴![]() (4+m)(6﹣
(4+m)(6﹣![]() m2+4m﹣6)﹣
m2+4m﹣6)﹣![]() ×4×6﹣
×4×6﹣![]() m(﹣
m(﹣![]() m2+4m﹣6)=12,
m2+4m﹣6)=12,
化簡得:m2﹣11m+24=0,解得m1=3,m2=8(舍),
∴點E的坐標(biāo)為(3,﹣![]() );
);
(3)①當(dāng)點Q在對稱軸右側(cè)時,如圖2,
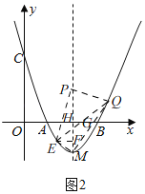
過點E作EF⊥PM于F,MQ交x軸于G,
∵∠PQE=∠PME,
∴點E,M,Q,P四點共圓,
∵PE⊥PQ,
∴∠EPQ=90°,
∴∠EMQ=90°,
∴∠EMF+∠HMG=90°,
∵∠HMG+∠HGM=90°,
∴∠EMF=∠HGM,
在Rt△EFM中,EF=1,FM=![]() ,tan∠EMF=
,tan∠EMF=![]() =2,
=2,
∴tan∠HGM=2,
∴![]() ,
,
∴HG=![]() HM=1,
HM=1,
∴點G(5,0),
∵M(4,﹣2),
∴直線MG的解析式為y=2x﹣10①,
∵二次函數(shù)解析式為y=![]() x2﹣4x+6②,
x2﹣4x+6②,
聯(lián)立①②解得,![]() (舍)或
(舍)或![]() ,
,
∴Q(8,6),
∴點Q到對稱軸的距離為8﹣4=4;
②當(dāng)點Q在對稱軸左側(cè)時,如圖3,
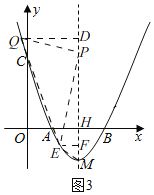
過點E作EF⊥PM于F,過點Q作QD⊥PM于D,
∴∠DQP+∠QPD=90°,
∵∠EPQ=90°,
∴∠DPQ+∠FPE=90°,
∴∠DQP=∠FPE,
∵∠PDQ=∠EFP,
∴△PDQ∽△EFP,
∴![]() ,
,
由①知,tan∠PQE=![]() =2,
=2,
∵EF=1,
∴![]() =
=![]() ,
,
∴DP=![]() ,PF=2QD,
,PF=2QD,
設(shè)Q(n,![]() n2﹣4n+6),
n2﹣4n+6),
∴DQ=4﹣n,DH=![]() n2﹣4n+6,
n2﹣4n+6,
∴PF=DH+FH﹣DP=![]() n2﹣4n+6+
n2﹣4n+6+![]() ﹣
﹣![]() =
=![]() n2﹣4n+7,
n2﹣4n+7,
∴![]() n2﹣4n+7=2(4﹣n),
n2﹣4n+7=2(4﹣n),
∴n=2+![]() (舍)或n=2﹣
(舍)或n=2﹣![]() ,
,
∴DQ=4﹣n=2+![]() ,
,
即點Q到對稱軸的距離為4或2+![]() .
.


科目:初中數(shù)學(xué) 來源: 題型:
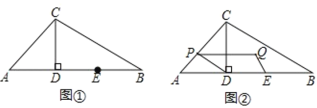
【題目】如圖①,在△ABC 中,CD⊥AB 于點 D,AD=CD=2,BD=4,點 E 是線段BD 的中點,點 P 從點 A 出發(fā),沿折線 AC-CB 向終點 B 運動,點 P 在邊 AC 上的速度為每秒![]() 個單位長度,P在BC邊上的速度為
個單位長度,P在BC邊上的速度為![]() 個單位長度,設(shè)P的運動時間為 t(秒).
個單位長度,設(shè)P的運動時間為 t(秒).
(1)用含 t 的代數(shù)式表示點 P 到直線 AB 的距離.
(2)如圖②,作點 P 關(guān)于直線 CD 的對稱點 Q,設(shè)以 D、E、Q、P 為頂點的四邊形的面積為 S(平方單位),求 S 與 t 之間的函數(shù)關(guān)系式.
(3)當(dāng)點 P 在邊 BC 上時,在△BCD 的邊上(不包括頂點)存在點 H,使四邊形 DEPH為軸對稱圖形,直接寫出此時線段 CP 的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,正方形ABCD的邊長為5,點A的坐標(biāo)為(﹣4,0),點B在y軸上,若反比例函數(shù)![]() (k≠0)的圖象過點C,則該反比例函數(shù)的表達式為( )
(k≠0)的圖象過點C,則該反比例函數(shù)的表達式為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
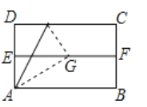
【題目】如圖,對折矩形紙片ABCD,使AB與DC重合得到折痕EF,將紙片展平,再一次折疊,使點D落到EF上點G處,并使折痕經(jīng)過點A,已知BC=2,則線段EG的長度為________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】有四張正面分別標(biāo)有數(shù)字![]() ,
,![]() ,
,![]() ,
,![]() 的不透明卡片,它們除數(shù)字不同外其余全部相同.現(xiàn)將它們背面朝上,洗勻后從中抽取一張,將該卡片上的數(shù)字記為
的不透明卡片,它們除數(shù)字不同外其余全部相同.現(xiàn)將它們背面朝上,洗勻后從中抽取一張,將該卡片上的數(shù)字記為![]() ;不放回,再從中抽取一張,將該卡片上的數(shù)字記為
;不放回,再從中抽取一張,將該卡片上的數(shù)字記為![]() ,則使關(guān)于
,則使關(guān)于![]() 的不等式組
的不等式組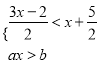 的解集中有且只有
的解集中有且只有![]() 個非負(fù)整數(shù)解的概率為 .
個非負(fù)整數(shù)解的概率為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】五名學(xué)生投籃球,每人投10次,統(tǒng)計他們每人投中的次數(shù).得到五個數(shù)據(jù),并對數(shù)據(jù)進行整理和分析給出如下信息:
平均數(shù) | 中位數(shù) | 眾數(shù) |
m | 6 | 7 |
則下列選項正確的是( )
A.可能會有學(xué)生投中了8次
B.五個數(shù)據(jù)之和的最大值可能為30
C.五個數(shù)據(jù)之和的最小值可能為20
D.平均數(shù)m一定滿足![]()
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在![]() 中,
中,![]() ,點D是
,點D是![]() 外一點,點D與點C在直線
外一點,點D與點C在直線![]() 的異側(cè),且點
的異側(cè),且點![]() 不共線,連接
不共線,連接![]() .
.


(1)如圖1,當(dāng)![]() 時,畫出圖形,直接寫出
時,畫出圖形,直接寫出![]() 之間的數(shù)量關(guān)系;
之間的數(shù)量關(guān)系;
(2)當(dāng)![]() 時,利用圖2,繼續(xù)探究
時,利用圖2,繼續(xù)探究![]() 之間的數(shù)量關(guān)系并證明;
之間的數(shù)量關(guān)系并證明;
(提示:嘗試運用圖形變換,將要研究的有關(guān)線段盡可能轉(zhuǎn)移到一個三角形中)
(3)當(dāng)![]() 時,進一步探究
時,進一步探究![]() 之間的數(shù)量關(guān)系,并用含
之間的數(shù)量關(guān)系,并用含![]() 的等式直接表示出它們之間的關(guān)系.
的等式直接表示出它們之間的關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() .
.
(1)求點![]() 的坐標(biāo)(用含
的坐標(biāo)(用含![]() 的式子表示);
的式子表示);
(2)求拋物線與![]() 軸的交點坐標(biāo);
軸的交點坐標(biāo);
(3)已知點![]() ,
,![]() ,如果拋物線與線段
,如果拋物線與線段![]() 恰有一個公共點,結(jié)合函數(shù)圖象,求
恰有一個公共點,結(jié)合函數(shù)圖象,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,線段
中,線段![]() 的垂直平分線交
的垂直平分線交![]() 于
于![]() ,分別交
,分別交![]() 于
于![]() ,連接
,連接![]() .
.
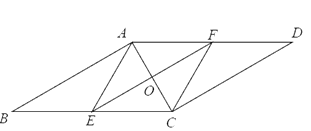
(1)證明:四邊形![]() 是菱形;
是菱形;
(2)在(1)的條件下,如果![]() ,求四邊形
,求四邊形![]() 的面積.
的面積.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com