
【題目】為了豐富同學們的課余生活,某學校計劃舉行社會實踐活動,現隨機抽取了部分學生進行主題為“你最想去的地點是?”的問卷調查,要求學生必須從“A(大鵬所城),B(園山),C(西沖),D(歡樂谷)”四個景點中選擇一項,根據調查結果,繪制了如圖兩幅不完整的統計圖,請你根據圖中所提供的信息,完成下列問題:
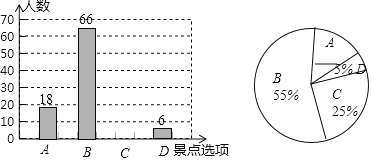
(1)本次調查的學生人數為 人;
(2)在扇形統計圖中,“園山”部分所占圓心角的度數為 ;
(3)請將兩幅統計圖補充完整;
(4)若該校共有3000名學生,估計該校最想去大鵬所城的學生人數約為多少人?
【答案】(1)120;(2)198°;(3)補全統計圖見解析;(4)750人.
【解析】
(1)由![]() 的人數除以其人數占被調查人數的百分比即可求解;
的人數除以其人數占被調查人數的百分比即可求解;
(2)用![]() “園山”部分所占的百分比即可求解;
“園山”部分所占的百分比即可求解;
(3)用調查的學生總人數乘以![]() 所占百分比得出
所占百分比得出![]() 的人數,補全條形圖;用1減去
的人數,補全條形圖;用1減去![]() 、
、![]() 、
、![]() 所占的百分比得出
所占的百分比得出![]() 所占的百分比,補全扇形圖;
所占的百分比,補全扇形圖;
(4)用樣本中最想去大鵬所城的學生所占的百分比乘總人數即可.
解:(1)本次調查的學生人數為![]() (人
(人![]() .
.
故答案為:120;
(2)在扇形統計圖中,“園山”部分所占圓心角的度數為:![]() .
.
故答案為![]() ;
;
(3)選擇![]() 的人數為:
的人數為:![]() (人
(人![]() ,
,
![]() 所占的百分比為:
所占的百分比為:![]() .
.
補全統計圖如圖:
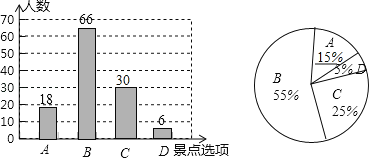
(4)根據題意得:
![]() (人
(人![]() .
.
答:估計該校最想去大鵬所城的學生人數約為750人.


科目:初中數學 來源: 題型:
【題目】正方形![]() 、正方形
、正方形![]() 如圖放置,點
如圖放置,點![]() 在同一條直線上,點
在同一條直線上,點![]() 在
在![]() 邊上,
邊上,![]() ,且
,且![]() ,連結
,連結![]() 交
交![]() 于
于![]() ,有下列結論:①
,有下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .以上結論正確的個數有( )
.以上結論正確的個數有( )
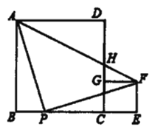
A.5個B.4個C.3個D.2個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在銳角![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 按逆時針方向旋轉,得到
按逆時針方向旋轉,得到![]() .
.
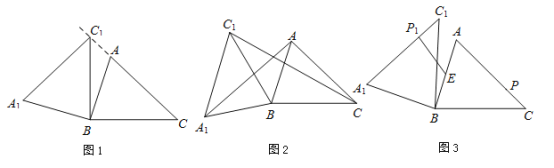
(1)如圖1,當點![]() 在線段
在線段![]() 的延長線上時,求
的延長線上時,求![]() 的度數;
的度數;
(2)如圖2,連接![]() ,
,![]() .若
.若![]() 的面積為4,求
的面積為4,求![]() 的面積;
的面積;
(3)如圖3,點![]() 為線段
為線段![]() 中點,點
中點,點![]() 是線段
是線段![]() 上的動點,在
上的動點,在![]() 繞點
繞點![]() 按逆時針方向旋轉過程中,點
按逆時針方向旋轉過程中,點![]() 的對應點是點
的對應點是點![]() ,求線段
,求線段![]() 長度的最小值.
長度的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知△ABC是邊長為![]() 的等邊三角形.將△ABC繞點A逆時針旋轉角θ(0°<θ<180°),得到△ADE,BD和EC所在直線相交于點O.
的等邊三角形.將△ABC繞點A逆時針旋轉角θ(0°<θ<180°),得到△ADE,BD和EC所在直線相交于點O.
(1)如圖a,當θ=20°時,判斷△ABD與△ACE是否全等?并說明理由;
(2)當△ABC旋轉到如圖b所在位置時(60°<θ<120°),求∠BOE的度數;
(3)在θ從60°到120°的旋轉過程中,點O運動的軌跡長為 .


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某飾品店老板去批發市場購買新款手鏈,第一次購手鏈共用1000元,將該手鏈以每條定價28元銷售,并很快售完,所得利潤率高于30%.由于該手鏈深得年輕人喜愛,十分暢銷,第二次去購進手鏈時,每條的批發價已比第一次高5元,共用去了1500元,所購數量比第一次多10條.當這批手鏈以每條定價32元售出80%時,出現滯銷,便以5折價格售完剩余的手鏈.現假設第一次購進手鏈的批發價為x元/條.
(1)用含x的代數式表示:第一次購進手鏈的數量為 條;
(2)求x的值;
(3)不考慮其他因素情況下,試問該老板第二次售手鏈是賠錢了,還是賺錢了?若賠錢,賠多少?若賺錢,賺多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
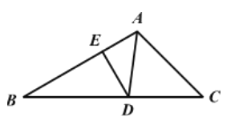
【題目】如圖,在△ABC中,∠B=30°,∠C=45°,AD平分∠BAC交BC于點D,DE⊥AB,垂足為E。若DE=1,則BC的長為( )
A.2+![]() B.
B.![]() C.
C.![]() D.3
D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
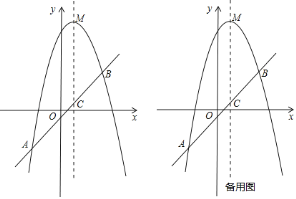
【題目】已知,如圖,拋物線![]() 的頂點為
的頂點為![]() ,經過拋物線上的兩點
,經過拋物線上的兩點![]() 和
和![]() 的直線交拋物線的對稱軸于點
的直線交拋物線的對稱軸于點![]() .
.
(1)求拋物線的解析式和直線![]() 的解析式.
的解析式.
(2)在拋物線上![]() 兩點之間的部分(不包含
兩點之間的部分(不包含![]() 兩點),是否存在點
兩點),是否存在點![]() ,使得
,使得![]() ?若存在,求出點
?若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
(3)若點![]() 在拋物線上,點
在拋物線上,點![]() 在
在![]() 軸上,當以點
軸上,當以點![]() 為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點
為頂點的四邊形是平行四邊形時,直接寫出滿足條件的點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
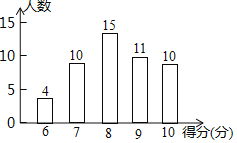
【題目】為了了解居民的環保意識,社區工作人員在光明小區隨機抽取了若干名居民開展主題為“打贏藍天保衛戰”的環保知識有獎問答活動,并用得到的數據繪制了如圖條形統計圖(得分為整數,滿分為10分,最低分為6分)
請根據圖中信息,解答下列問題:
(1)本次調查一共抽取了 名居民;
(2)求本次調查獲取的樣本數據的平均數、眾數和中位數;
(3)社區決定對該小區500名居民開展這項有獎問答活動,得10分者設為“一等獎”,請你根據調查結果,幫社區工作人員估計需準備多少份“一等獎”獎品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:有三條邊相等的四邊形稱為三等邊四邊形.
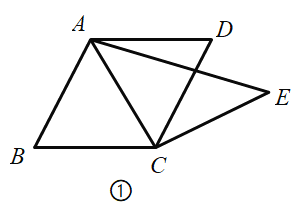
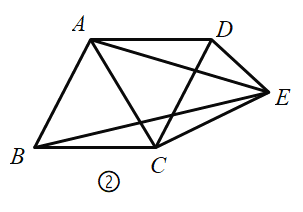
(1)如圖①,平行四邊形![]() 中,對角線
中,對角線![]() 平分
平分![]() ,將線段
,將線段![]() 繞點
繞點![]() 旋轉一個角度
旋轉一個角度![]() 至
至![]() ,連接
,連接![]() .
.
①求證:四邊形![]() 是三等邊四邊形;
是三等邊四邊形;
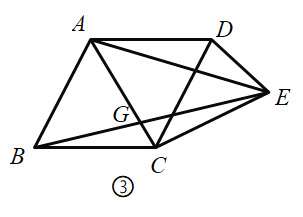
②如圖②,連接![]() ,
,![]() .求證:
.求證:![]() ;
;
(2)如圖,在(1)的條件下,設![]() 與
與![]() 交于點
交于點![]() ,
,![]() ,
,![]() ,
,![]() ,求以
,求以![]() ,
,![]() 和
和![]() 為邊的三角形的面積.
為邊的三角形的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com