
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,且
,且![]() 面積是24,
面積是24,![]() 的垂直平分線
的垂直平分線![]() 分別交
分別交![]() 邊于點
邊于點![]() ,若點
,若點![]() 為
為![]() 邊的中點,點
邊的中點,點![]() 為線段
為線段![]() 上一動點,則
上一動點,則![]() 周長的最小值為( )
周長的最小值為( )

A.9B.10C.11D.12
【答案】C
【解析】
連接AD,AM,由于△ABC是等腰三角形,點D是BC邊的中點,故AD⊥BC,再根據三角形的面積公式求出AD的長,再根據EF是線段AC的垂直平分線可知,點A關于直線EF的對稱點為點C,MA=MC,推出MC+DM=MA+DM≥AD,故AD的長為BM+MD的最小值,由此即可得出結論.
連接AD,MA.
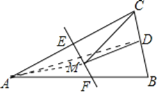
∵△ABC是等腰三角形,點D是BC邊的中點,
∴AD⊥BC,
∴S△ABC=![]() BCAD=
BCAD=![]() ×6×AD=24,解得AD=8,
×6×AD=24,解得AD=8,
∵EF是線段AC的垂直平分線,
∴點A關于直線EF的對稱點為點C,MA=MC,
∴MC+DM=MA+DM≥AD,
∴AD的長為CM+MD的最小值,
∴△CDM的周長最短=(CM+MD)+CD=AD+![]() BC=8+
BC=8+![]() ×6=8+3=11.
×6=8+3=11.
故選:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】二次根式的化簡中,若被開方數還有根號,有的能將被開方數化成另一個二次根式的平方的形式,比如:![]() ,聰明的你可以繼續探究,當a,b,m,n為正整數時,若
,聰明的你可以繼續探究,當a,b,m,n為正整數時,若![]() ,則有
,則有![]() ,所以
,所以![]() .模仿上述探究解決下列問題:
.模仿上述探究解決下列問題:
(1)當a,b,m,n為正整數時,![]() ,請用含m,n的代數式分別表示a,b:a= ,b= .
,請用含m,n的代數式分別表示a,b:a= ,b= .
(2)填空:![]() =( +
=( + ![]() )2
)2
(3)若![]() ,且a,m,n均為正整數,求a的值.
,且a,m,n均為正整數,求a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們新定義一種三角形:兩邊平方和等于第三邊平方的4倍的三角形叫做常態三角形.例如:某三角形三邊長分別是5,6和8,因為![]() ,所以這個三角形是常態三角形.
,所以這個三角形是常態三角形.
(1)若![]() 三邊長分別是2,
三邊長分別是2,![]() 和4,則此三角形 常態三角形(填“是”或“不是”
和4,則此三角形 常態三角形(填“是”或“不是” ![]() ;
;
(2)如圖,![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 的中點,連接
的中點,連接![]() ,若
,若![]() 是常態三角形,求
是常態三角形,求![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,經過點B(﹣2,0)的直線y=kx+b與直線y=4x+2相交于點A(﹣1,﹣2),4x+2<kx+b<0的解集為( )
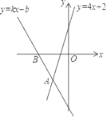
A.x<﹣2B.﹣2<x<﹣1C.x<﹣1D.x>﹣1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】今年汶川車厘子喜獲豐收,車厘子一上市,水果店的王老板用2500元購進一批車厘子,很快售完;老板又用4400元購進第二批車厘子,所購數量是第一批的2倍,由于進貨量增加,進價比第一批每干克少了3元.”
(l)第一批車厘子每千克進價多少元?.
(2)該老板在銷售第二批車厘子時,售價在第二批進價的基礎上增加了![]() ,售出
,售出![]() 后,為了盡快售完,決定將剩余車厘子在第二批進價的基礎上每千克降價
后,為了盡快售完,決定將剩余車厘子在第二批進價的基礎上每千克降價![]() 元進行促銷,結果第二批車厘子的銷售利潤為1520元,求
元進行促銷,結果第二批車厘子的銷售利潤為1520元,求![]() 的值。(利潤=售價一進價)
的值。(利潤=售價一進價)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們知道整數![]() 除以整數
除以整數![]() (其中
(其中![]() ),可以用豎式計算,例如計算
),可以用豎式計算,例如計算![]() 可以用整式除法如圖:
可以用整式除法如圖:![]() ,所以
,所以![]() .
.
類比此方法,多項式除以多項式一般也可以用豎式計算,步驟如下:
①把被除式,除式按某個字母作降冪排列,并把所缺的項用零補齊;
②用被除式的第一項除以除式第一項,得到商式的第一項;
③用商式的第一項去乘除式,把積寫在被除式下面(同類對齊),消去相等項;
④把減得的差當作新的被除式,再按照上面的方法繼續演算,直到余式為零或余式的次數低于除式的次數時為止,被除式=除式×商式+余式,若余式為零,說明這個多項式能被另一個多項式整除.
例如:計算![]() .
.
可用整式除法如圖:

所以![]() 除以
除以![]()
商式為![]() ,余式為0
,余式為0
根據閱讀材料,請回答下列問題:
(1)![]() .
.
(2)![]() ,商式為 ,余式為 .
,商式為 ,余式為 .
(3)若關于![]() 的多項式
的多項式![]() 能被三項式
能被三項式![]() 整除,且
整除,且![]() 均為整數,求滿足以上條件的
均為整數,求滿足以上條件的![]() 的值及商式.
的值及商式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,以點P(﹣1,0)為圓心的圓,交x軸于B、C兩點(B在C的左側),交y軸于A、D兩點(A在D的下方),AD=2,將△ABC繞點P旋轉180°,得到△MCB.
(1)求B、C兩點的坐標;
(2)請在圖中畫出線段MB、MC,并判斷四邊形ACMB的形狀(不必證明),求出點M的坐標;
(3)動直線l從與BM重合的位置開始繞點B順時針旋轉,到與BC重合時停止,設直線l與CM交點為E,點Q為BE的中點,過點E作EG⊥BC于G,連接MQ、QG.請問在旋轉過程中∠MQG的大小是否變化?若不變,求出∠MQG的度數;若變化,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com