
【題目】如圖1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,點P從點C出發沿線段CA以每秒2cm的速度運動,同時點Q從點B出發沿線段BC以每秒1cm的速度運動.設運動時間為t秒(0<t<5).
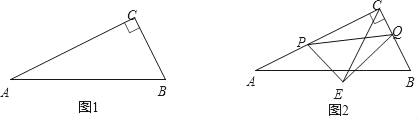
(1)填空:AB= cm;
(2)t為何值時,△PCQ與△ACB相似;
(3)如圖2,以PQ為斜邊在異于點C的一側作Rt△PEQ,且![]() ,連結CE,求CE.(用t的代數式表示).
,連結CE,求CE.(用t的代數式表示).
【答案】(1)![]() cm;(2)當t=1或
cm;(2)當t=1或![]() 秒時,△PCQ與△ACB相似;(3)CE=3+t;
秒時,△PCQ與△ACB相似;(3)CE=3+t;
【解析】
(1)利用勾股定理可求得AB.
(2)分![]() 和
和![]() 兩種情況討論.
兩種情況討論.
(3) 過點![]() 作
作![]() 交
交![]() 于
于![]() ,先說明△
,先說明△![]() ∽△
∽△![]() ,得到
,得到![]() ,用含t的代數式表示HE、CH,最后用勾股定理求出CE.
,用含t的代數式表示HE、CH,最后用勾股定理求出CE.
(1)AB=![]() cm;
cm;
(2)由題意可知:![]() ,
,![]() ,QC=5-t
,QC=5-t
∵∠PCQ=∠ACB
∴當![]() 或
或![]() 時,△PCQ與△ACB相似
時,△PCQ與△ACB相似
當![]() 時,
時,![]() ,解得t=1;
,解得t=1;
當![]() 時,
時,![]() ,解得t=
,解得t=![]() ,
,
![]() 當t=1或
當t=1或![]() 秒時,△PCQ與△ACB相似;
秒時,△PCQ與△ACB相似;
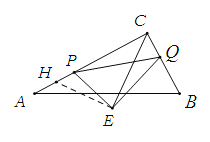
(3)如圖,過點![]() 作
作![]() 交
交![]() 于
于![]() ,則
,則![]()
![]()
![]() 即
即![]()
∴![]()
∵![]()
∴![]()
![]() △
△![]() ∽△
∽△![]()
∴![]()
∴![]() ,
,![]()
∴![]()
在![]() 中,
中,![]() ,
,
即![]()
∴![]()
∴![]()
故答案為:(1)![]() cm;(2)當t=1或
cm;(2)當t=1或![]() 秒時,△PCQ與△ACB相似;(3)CE=3+t.
秒時,△PCQ與△ACB相似;(3)CE=3+t.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,已知正比例函數y=![]() x的圖象與反比例函數y=
x的圖象與反比例函數y=![]() 的圖象交于A(a,-2),B兩點.
的圖象交于A(a,-2),B兩點.
(1)求反比例函數的表達式和點B的坐標;
(2)P是第一象限內反比例函數圖象上一點,過點P作y軸的平行線,交直線AB于點C,連接PO,若△POC的面積為3,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
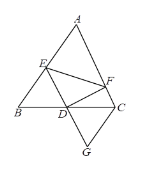
【題目】如圖,在△ABC中,D為BC的中點,E為AB上一點,DF⊥DE交AC于點F,延長ED至點G,使GD=ED,連接CG.
(1)求證:BE=CG;
(2)求證:BE+CF>EF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】關于x的一元二次方程x2+(k﹣5)x+1﹣k=0,其中k為常數.
(1)求證:無論k為何值,方程總有兩個不相等實數根;
(2)若原方程的一根大于3,另一根小于3,求k的最大整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
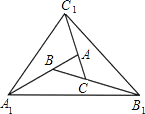
【題目】如圖,對面積為1的△ABC逐次進行以下操作:第一次操作,分別延長AB、BC、CA至點A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,順次連接A1、B1、C1得到△A1B1C1,記其面積為S1;第二次操作,分別延長A1B1、B1C1、C1A1至點A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,順次連按A2、B2、C2,得到△A2B2C2,記其面積為S2;按此規律繼續下去,可得到△A2019B2019C2019,則其面積S2019=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰△ABC中,AB=BC,以BC為直徑的⊙O與AC相交于點D,過點D作DE⊥AB交CB延長線于點E,垂足為點F.
(1)判斷DE與⊙O的位置關系,并說明理由;
(2)若⊙O的半徑R=5,tanC=![]() ,求EF的長.
,求EF的長.
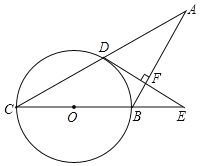
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著“互聯網+”時代的到來,一種新型打車方式受到大眾歡迎,該打車方式的總費用由里程費和耗時費組成,其中里程費按x元/公里計算,耗時費按y元/分鐘計算(總費用不足9元按9元計價).小明、小剛兩人用該打車方式出行,按上述計價規則,其打車總費用、行駛里程數與打車時間如表:
時間(分鐘) | 里程數(公里) | 車費(元) | |
小明 | 8 | 8 | 12 |
小剛 | 12 | 10 | 16 |
(1)求x,y的值;
(2)如果小華也用該打車方式,打車行駛了11公里,用了14分鐘,那么小華的打車總費用為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某活動小組為了估計裝有![]() 個白球和若干個紅球(每個球除顏色外都相同)的袋中紅球接近多少個,在不將袋中球倒出來的情況下,分小組進行摸球試驗,兩人一組,共
個白球和若干個紅球(每個球除顏色外都相同)的袋中紅球接近多少個,在不將袋中球倒出來的情況下,分小組進行摸球試驗,兩人一組,共![]() 組進行摸球實驗.其中一位學生摸球,另一位學生記錄所摸球的顏色,并將球放回袋中搖勻,每一組做
組進行摸球實驗.其中一位學生摸球,另一位學生記錄所摸球的顏色,并將球放回袋中搖勻,每一組做![]() 次試驗,匯總起來后,摸到紅球次數為
次試驗,匯總起來后,摸到紅球次數為![]() 次.
次.
![]() 估計從袋中任意摸出一個球,恰好是紅球的概率是多少?
估計從袋中任意摸出一個球,恰好是紅球的概率是多少?
![]() 請你估計袋中紅球接近多少個?
請你估計袋中紅球接近多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com