
【題目】如圖甲,點C將線段AB分成兩部分(AC>BC),如果 ![]() =
= ![]() ,那么稱點C為線段AB的黃金分割點.某數學興趣小組在進行課題研究時,由黃金分割點聯想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成面積分別為S1 , S2(S1>S2)的兩部分,如果
,那么稱點C為線段AB的黃金分割點.某數學興趣小組在進行課題研究時,由黃金分割點聯想到“黃金分割線”,類似地給出“黃金分割線”的定義:直線l將一個面積為S的圖形分成面積分別為S1 , S2(S1>S2)的兩部分,如果 ![]() =
= ![]() ,那么稱直線l為該圖形的黃金分割線.
,那么稱直線l為該圖形的黃金分割線.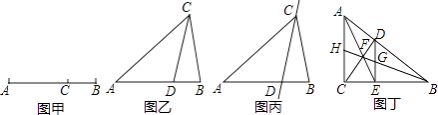
(1)如圖乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分線交AB于點D,請問點D是否是AB邊上的黃金分割點,并證明你的結論;
(2)若△ABC在(1)的條件下,如圖丙,請問直線CD是不是△ABC的黃金分割線,并證明你的結論;
(3)如圖丁,在Rt△ABC中,∠ACB=90°,D為斜邊AB上的一點,(不與A,B重合)過D作DE⊥BC于點E,連接AE,CD相交于點F,連接BF并延長,與DE,AC分別交于點G,H.請問直線BH是直角三角形ABC的黃金分割線嗎?并說明理由.
【答案】
(1)解:點D是AB邊上的黃金分割點.理由如下:
∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵CD是角平分線,
∴∠ACD=∠BCD=36°,
∴∠A=∠ACD,
∴AD=CD,
∵∠CDB=180°﹣∠B﹣∠BCD=72°,
∴∠CDB=∠B,
∴BC=CD,
∴BC=AD.
在△BCD與△BCA中,∠B=∠B,∠BCD=∠A=36°,
∴△BCD∽△BAC,
∴ ![]() ,
,
∴ ![]() ,
,
∴點D是AB邊上的黃金分割點.
(2)直線CD是△ABC的黃金分割線.理由如下:
證明:設△ABC中,AB邊上的高為h,則S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,
BDh,
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
由(1)知,點D是AB邊上的黃金分割點,
∴ ![]() ,
,
∴S△ACD:S△ABC=S△BCD:S△ACD,
∴CD是△ABC的黃金分割線.
(3)解:直線BH不是△ABC的黃金分割線.理由如下:
∵DE∥AC,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
, ![]() ,
,
∴ ![]() ,
,
∴AH2=HC2,
∴AH=HC,
∴S△BHA=S△BHC= ![]() S△ABC,
S△ABC,
∴BH不是△ABC的黃金分割線.
【解析】(1)根據等邊對等角得出∠B=∠ACB=72°,根據角平分線的定義及等量代換得出∠A=∠ACD,進而根據等角對等邊得出AD=CD,BC=CD,從而得出BC=AD.然后判斷出△BCD∽△BAC,根據相似三角形對應邊成比例得出![]() =
=![]() ,從而得出
,從而得出![]() =
=![]() ,從而得出結論點D是AB邊上的黃金分割點;
,從而得出結論點D是AB邊上的黃金分割點;
(2)設△ABC中,AB邊上的高為h,根據三角形的面積公式,則S△ABC= ![]() ABh,S△ACD=
ABh,S△ACD= ![]() ADh,S△BCD=
ADh,S△BCD= ![]() BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,點D是AB邊上的黃金分割點,故
BDh,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,點D是AB邊上的黃金分割點,故![]() =
=![]() ,根據等量代換得S△ACD:S△ABC=S△BCD:S△ACD,從而得出結論;
,根據等量代換得S△ACD:S△ABC=S△BCD:S△ACD,從而得出結論;
(3)直線BH不是△ABC的黃金分割線.理由如下:根據平行線分線段成比例定理得出AH2=HC2,故AH=HC,從而S△BHA=S△BHC= ![]() S△ABC,得出結論BH不是△ABC的黃金分割線.
S△ABC,得出結論BH不是△ABC的黃金分割線.
【考點精析】通過靈活運用三角形的面積和平行線分線段成比例,掌握三角形的面積=1/2×底×高;三條平行線截兩條直線,所得的對應線段成比例即可以解答此題.


 優學名師名題系列答案
優學名師名題系列答案科目:初中數學 來源: 題型:
【題目】已知下列方程:①![]() ;②0.3x=1;③
;②0.3x=1;③![]() ;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的個數是( )
;④x2﹣4x=3;⑤x=6;⑥x+2y=0.其中一元一次方程的個數是( )
A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為一位旅行者在早晨8時從城市出發到郊外所走路程與時間的變化圖.根據圖回答問題:
(1)9時,10時30分,12時所走的路程分別是多少千米?
(2)他中途休息了多長時間?
(3)他從休息后直達目的地這段時間的速度是多少?(列式計算)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算
(1)(6x4﹣4x3+2x2)÷(﹣2x2)+3x2
(2)(x﹣5)(2x+5)+2x(3﹣x)
(3)(﹣1)2016+(﹣![]() )﹣2﹣(3.14﹣π)0
)﹣2﹣(3.14﹣π)0
(4)運用乘法公式計算:1122﹣113×111
查看答案和解析>>
科目:初中數學 來源: 題型:
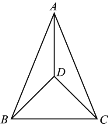
【題目】如圖,在△ABC中,AB=AC,D是三角形內一點,連接AD,BD,CD,∠BDC=90°,∠DBC=45°.
(1)求證:∠BAD=∠CAD;
(2)求∠ADB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=k1x+b與反比例函數y= ![]() (x>0)的圖象交于A(1,6),B(a,3)兩點.
(x>0)的圖象交于A(1,6),B(a,3)兩點.
(1)求k1和k2的值;
(2)結合圖象直接寫出k1x+b﹣ ![]() >0的x的取值范圍.
>0的x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,數軸上的點A、B分別表示數a、b,則點A、B(點B在點A的右側)之間的距離表示為AB=b﹣a,若點C對應的數為c,滿足|a+3|+(c﹣9)2=0.
(1)寫出AC的值 .
(2)如圖②,點D在點C的右側且距離m(m>0)個單位,點B在線段AC上,滿足AB+AC=BD,求AB的值(用含有m的代數式表示).
(3)如圖③,若點D在點C的右側6個單位處,點P從點A出發以2個單位/秒的速度向右運動,同時點M從點C出發以1個單位/秒的速度也向右運動,當到達D點后以原來的速度向相反的方向運動.求經過多長時間,點P和點M之間的距離是2個單位?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com