
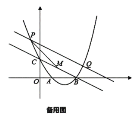
【題目】拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于
軸交于![]() ,其中
,其中![]() ,點
,點![]() 為拋物線上一動點,過點
為拋物線上一動點,過點![]() 作
作![]() 平行
平行![]() 交拋物線于
交拋物線于![]() ,
,
(1)求拋物線的解析式;
(2)①當![]() 兩點重合時時,
兩點重合時時,![]() 所在直線解析式為_____________.
所在直線解析式為_____________.
②在①的條件下,取線段![]() 中點
中點![]() ,連接
,連接![]() ,判斷以點
,判斷以點![]() 為頂點的四邊形是什么四邊形,并說明理由?
為頂點的四邊形是什么四邊形,并說明理由?
(3)已知 ,連接
,連接![]() ,
,![]() 軸,交
軸,交![]() 于
于![]() ,
,![]() 軸上有一動點
軸上有一動點![]() ,
,![]() ,
,![]() 的長為______.
的長為______.

【答案】(1)![]() ;(2)①
;(2)①![]() ,②菱形,見解析;(3)
,②菱形,見解析;(3)![]() 或
或![]()
【解析】
(1)將![]() 代入
代入![]() 即可解答;
即可解答;
(2)①待定系數法求出直線BC的解析式,當![]() 兩點重合時,即直線與拋物線只有一個交點,結合直線PQ∥BC,即可設直線PQ為
兩點重合時,即直線與拋物線只有一個交點,結合直線PQ∥BC,即可設直線PQ為![]() ,聯立拋物線解析式,根據根的判別式即可求出m的值,進而得到直線PQ的解析式;
,聯立拋物線解析式,根據根的判別式即可求出m的值,進而得到直線PQ的解析式;
②畫出圖形,根據M是BC的中點,計算出BM=![]() ,聯立方程組求出點P的坐標,得到OP=
,聯立方程組求出點P的坐標,得到OP=![]() ,從而證明四邊形POMB是平行四邊形,再根據OP=OM,從而證明平行四邊形POMB是菱形即可;
,從而證明四邊形POMB是平行四邊形,再根據OP=OM,從而證明平行四邊形POMB是菱形即可;
(3)求出直線BN的解析式,得出點E的坐標以及∠ONB=60°,∠OBN=30°,如圖所示,以NE為邊,∠ONB為內角,構造等邊△HNE,并作△HNE的外接圓圓P,交x軸于點F1,F2,連接NP,EP,NF1,EF1,NF2,EF2,根據同圓中等弦所對的圓周角相等,即可確定∠NF1E=∠NF2E=∠NHE=60°,從而確定點F,根據∠PNE=∠PEN=30°,∠PEN=∠OBN=30°,得到PE∥OB,結合PN=PE,列出方程,求出點P的坐標,再由垂徑定理即可求出![]() ,從而得出OF1及OF2即可.
,從而得出OF1及OF2即可.
解:(1)將![]() 代入
代入![]() 得:
得:
 ,解得:
,解得: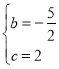 ,
,
∴![]() ;
;
(2)①設直線BC的解析式為y=kx+a,將![]() 代入得:
代入得:
![]() ,解得:
,解得: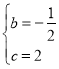 ,
,
∴直線BC為:![]() ,
,
當![]() 兩點重合時,即直線與拋物線只有一個交點,
兩點重合時,即直線與拋物線只有一個交點,
∵直線PQ∥BC,
∴設直線PQ的解析式為![]() ,
,
由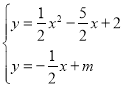 ,得
,得![]() ,
,
∴![]() ,解得m=0,
,解得m=0,
∴直線PQ的解析式為![]() ,
,
故答案為:![]() ;
;
②如圖,∵![]() ,點M是BC的中點,
,點M是BC的中點,
∴M(2,1)
∴BM=![]() ,OM=
,OM=![]() ,
,
由 得
得![]() ,
,
∴P(2,-1),
∴OP=![]() ,
,
∵直線PQ經過原點,
∴OP∥BM,
又∵OP=BM,
∴四邊形POMB是平行四邊形,
又∵OP=OM=![]() ,
,
∴平行四邊形POMB是菱形;
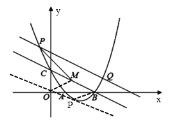
(3)設直線BN的解析式為y=px+q,
將![]() ,
,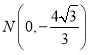 代入得:
代入得:
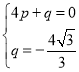 ,解得:
,解得: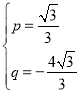 ,
,
∴直線BN的解析式為:![]() ,
,
當x=3時,y=![]() ,
,
∴E![]() ,
,
∵OB=4,ON=![]() ,
,
∴tan∠ONB=![]() ,
,
∴∠ONB=60°,則∠OBN=30°,
如圖所示,以NE為邊,∠ONB為內角,構造等邊△HNE,并作△HNE的外接圓圓P,交x軸于點F1,F2,連接NP,EP,NF1,EF1,NF2,EF2,
∴∠NF1E=∠NF2E=∠NHE=60°,
∵點P是△HNE的外接圓圓心,
∴NP,PE分別平分∠ONE,∠HEN,
∴∠PNE=∠PEN=30°,
∴∠PEN=∠OBN=30°,
∴PE∥OB,
∴點P的縱坐標為![]() ,
,
設點P為![]() ,
,
∵PN=PE,
∴![]() ,解得:n=1,
,解得:n=1,
∴P![]() ,
,
∴圓P的半徑為PE=2,
過點P作PG⊥x軸于點G,連接PF1,
則GP=![]() ,OG=1,PF1=2,
,OG=1,PF1=2,
由垂徑定理得: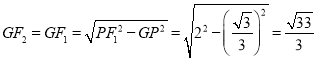 ,
,
∴OF1=GF1-OG=![]() =
=![]() ,OF2=GF2+OG=
,OF2=GF2+OG=![]() =
=![]() ,
,
故答案為:![]() 或
或![]() .
.



科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后得到
后得到![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到線段
后得到線段![]() ,分別以
,分別以![]() 、
、![]() 為圓心,
為圓心,![]() 、
、![]() 長為半徑畫弧
長為半徑畫弧![]() 和弧
和弧![]() ,連接
,連接![]() ,則圖中陰影部分的面積是________.
,則圖中陰影部分的面積是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春臨大地,學校決定給長12米,寬9米的一塊長方形展示區進行種植改造現將其劃分成如圖兩個區域:區域Ⅰ矩形ABCD部分和區域Ⅱ四周環形部分,其中區域Ⅰ用甲、乙、丙三種花卉種植,且EF平分BD,G,H分別為AB,CD中點.
(1)若區域Ⅰ的面積為Sm2,種植均價為180元/m2,區域Ⅱ的草坪均價為40元/m2,且兩區域的總價為16500元,求S的值.
(2)若AB:BC=4:5,區域Ⅱ左右兩側草坪環寬相等,均為上、下草坪環寬的2倍
①求AB,BC的長;
②若甲、丙單價和為360元/m2,乙、丙單價比為13:12,三種花卉單價均為20的整數倍.當矩形ABCD中花卉的種植總價為14520元時,求種植乙花卉的總價.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某同學報名參加校運動會,有以下5個項目可供選擇:徑賽項目:100m,200m,![]() 分別用
分別用![]() 、
、![]() 、
、![]() 表示
表示![]() ;田賽項目:跳遠,跳高
;田賽項目:跳遠,跳高![]() 分別用
分別用![]() 、
、![]() 表示
表示![]() .
.
![]() 該同學從5個項目中任選一個,恰好是田賽項目的概率為______;
該同學從5個項目中任選一個,恰好是田賽項目的概率為______;
![]() 該同學從5個項目中任選兩個,利用樹狀圖或表格列舉出所有可能出現的結果,并求恰好是一個田賽項目和一個徑賽項目的概率.
該同學從5個項目中任選兩個,利用樹狀圖或表格列舉出所有可能出現的結果,并求恰好是一個田賽項目和一個徑賽項目的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市為開發沿黃流域小白河漁業資源,鼓勵養殖戶開展混合養殖,現公布如下政策:![]() 每畝水面年租金為
每畝水面年租金為![]() 元;
元;![]() 每畝水面可在年初混合投放
每畝水面可在年初混合投放![]() 公斤甲種魚和
公斤甲種魚和![]() 公斤乙種魚:經市場調查發現:每公斤甲種魚的價格為
公斤乙種魚:經市場調查發現:每公斤甲種魚的價格為![]() 元,每公斤甲種魚的飼養費用為
元,每公斤甲種魚的飼養費用為![]() 元,每公斤甲種魚當年可獲
元,每公斤甲種魚當年可獲![]() 元收益;每公斤乙種魚的價格為
元收益;每公斤乙種魚的價格為![]() 元,每公斤乙種魚的飼養費用為
元,每公斤乙種魚的飼養費用為![]() 元,每公斤乙種魚當年可獲
元,每公斤乙種魚當年可獲![]() 元收益;
元收益;
(1)某養殖戶現有資金![]() 元,他準備再向銀行貸款,用于甲乙魚混合養殖,已知銀行貸款的年利率為
元,他準備再向銀行貸款,用于甲乙魚混合養殖,已知銀行貸款的年利率為![]() ,試問該養殖戶至少應租多少畝水面,并至少向銀行貸款多少元,可使年利潤不少于
,試問該養殖戶至少應租多少畝水面,并至少向銀行貸款多少元,可使年利潤不少于![]() 元?
元?
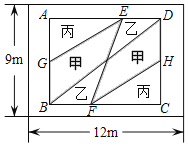
(2)為了節省材料該養殖戶利用河岸的一角![]() 的兩邊為邊,用總長為
的兩邊為邊,用總長為![]() 米的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形
米的圍網在水庫中圍成了如圖所示的①②③三塊區域,其中區域①為直角三角形,區域②③為矩形,而且四邊形![]() 為直角梯形.
為直角梯形.
I.若①②③這塊區域的面積相等,則![]() 的長為 米;
的長為 米;
II.設![]() 四邊形
四邊形![]() 的面積為
的面積為![]() 求
求![]() 與
與![]() 之的函數關系式,并說明
之的函數關系式,并說明![]() 為何值時,
為何值時,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年4月23日是世界讀書日,某校為了解學生課外閱讀情況,隨機抽取![]() 名學生,對每人每周用于課外閱讀的平均時間(單位:
名學生,對每人每周用于課外閱讀的平均時間(單位:![]() )進行調查,過程如下:
)進行調查,過程如下:
收集數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理數據:
課外閱讀平均時間 |
|
|
|
|
等級 |
|
|
|
|
人數 |
|
|
|
|
分析數據:
平均數 | 中位數 | 眾數 |
|
|
|
請根據以上提供的信息,解答下列問題:
(1)填空:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)已知該校學生![]() 人,若每人每周用于課外閱讀的平均時間不少于
人,若每人每周用于課外閱讀的平均時間不少于![]() 為達標,請估計達標的學生數;
為達標,請估計達標的學生數;
查看答案和解析>>
科目:初中數學 來源: 題型:
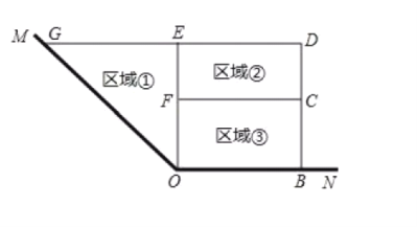
【題目】如圖,在Rt△ABC中,∠C=90°,AD平分∠BAC,交BC于點D,點O在AB上,⊙O經過A,D兩點,交AB于點E,交AC于點F
(1)求證:BC是⊙O的切線;
(2)若⊙O半徑是2cm,F是弧AD的中點,求陰影部分的面積(結果保留π和根號)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com