
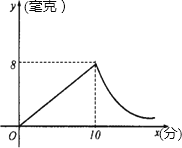
【題目】為預防“手足口病”,某校對教室進行“藥熏消毒”.已知藥物燃燒階段,室內每立方米空氣中的含藥量y(毫克)與燃燒時間x(分鐘)成正比例;燃燒階段后,y與x成反比例(這兩個變量之間的關系如圖所示).現測得藥物10分鐘燃完,此時教室內每立方米空氣含藥量為8毫克.據以上信息解答下列問題:
(1)求藥物燃燒時y與x的函數解析式.
(2)求藥物燃燒階段后y與x的函數解析式.
(3)當“藥熏消毒”時間到50分鐘時,每立方米空氣中的含藥量對人體方能無毒害作用,那么當“藥熏消毒”時間到50分鐘時每立方米空氣中的含藥量為多少毫克?
【答案】(1) 藥物燃燒階段的函數解析式為y=![]() x;(2)藥物燃燒階段后的函數解析式為y=
x;(2)藥物燃燒階段后的函數解析式為y=![]() ;(3)當“藥熏消毒”時間到50分鐘時每立方米空氣中的含藥量為1.6毫克.
;(3)當“藥熏消毒”時間到50分鐘時每立方米空氣中的含藥量為1.6毫克.
【解析】
(1)由于在藥物燃燒階段,y與x成正比例,因此設函數解析式為y=k1x(k1≠0),然后由(10,8)在函數圖象上,利用待定系數法即可求得藥物燃燒時y與x的函數解析式;
(2)由于在藥物燃燒階段后,y與x成反比例,因此設函數解析式為y=![]() (k2≠0),然后由(10,8)在函數圖象上,利用待定系數法即可求得藥物燃燒階段后y與x的函數解析式;
(k2≠0),然后由(10,8)在函數圖象上,利用待定系數法即可求得藥物燃燒階段后y與x的函數解析式;
(3)當“藥熏消毒”時間到50分鐘時,可知在藥物燃燒階段后,將x=50代入y=![]() ,即可求得y的值,則可求得答案.
,即可求得y的值,則可求得答案.
(1)由于在藥物燃燒階段,y與x成正比例,
因此設函數解析式為y=k1x(k1≠0),
由圖示可知,當x=10時,y=8.將x=10,y=8代入函數解析式,
解得k1=![]() .
.
∴藥物燃燒階段的函數解析式為y=![]() x.
x.
(2)由于在藥物燃燒階段后,y與x成反比例,因此設函數解析式為y=![]() (k2≠0),
(k2≠0),
同理將x=10,y=8代入函數解析式,解得k2=80.
∴藥物燃燒階段后的函數解析式為y=![]() .
.
(3)當x=50時,y=![]() =
=![]() =1.6.
=1.6.
∴當“藥熏消毒”時間到50分鐘時每立方米空氣中的含藥量為1.6毫克.


 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:初中數學 來源: 題型:
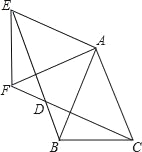
【題目】如圖,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC繞點A按順時針方向旋轉得到的,連接BE、CF相交于點D
(1)求證:BE=CF;
(2)當四邊形ACDE為平行四邊形時,求證:△ABE為等腰直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=﹣x2+2x.
(1)在給定的平面直角坐標系中,畫出這個函數的圖象;
(2)根據圖象,寫出當y<0時,x的取值范圍;
(3)若將此圖象沿x軸向左平移3個單位,再沿y軸向下平移1個單位,請直接寫出平移后圖象所對應的函數關系式.

查看答案和解析>>
科目:初中數學 來源: 題型:
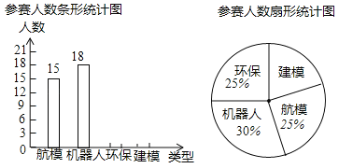
【題目】為了提高科技創新意識,我市某中學在“2018年科技節”活動中舉行科技比賽,包括“航模”、“機器人”、“環保”、“建模”四個類別(每個學生只能參加一個類別的比賽),各類別參賽人數統計如圖:
請根據以上信息,解答下列問題:
(1)全體參賽的學生共有 人,“建模”在扇形統計圖中的圓心角是 °;
(2)將條形統計圖補充完整;
(3)在比賽結果中,獲得“環保”類一等獎的學生為1名男生和2名女生,獲得“建模”類一等獎的學生為1名男生和1名女生,現從這兩類獲得一等獎的學生中各隨機選取1名學生參加市級“環保建模”考察活動,請用列表或畫樹狀圖的方法求選取的兩人中恰為1男生1女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校部分團員參加社會公益活動,準備購進一批許愿瓶進行銷售,并將所得利潤捐給慈善機構.根據市場調查,這種許愿瓶一段時間內的銷售量y(個)與銷售單價x(元/個)之間的對應關系如圖所示:
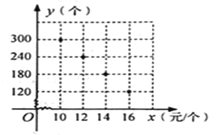
(1)試判斷y與x之間的函數關系,并求出函數關系式;
(2)若許愿瓶的進價為6元/個,按照上述市場調查的銷售規律,求銷售利潤w(元)與銷售單價x(元/個)之間的函數關系式;
(3)在(2)的條件下,若許愿瓶的進貨成本不超過900元,要想獲得最大的利潤,試確定這種許愿瓶的銷售單價,并求出此時的最大利潤.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=kx+b(k≠0)與雙曲線y=![]() (m≠0)相交于A(1,2),B(n,-1)兩點.
(m≠0)相交于A(1,2),B(n,-1)兩點.
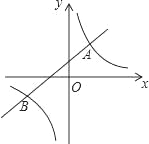
(1)求雙曲線的解析式;
(2)若A1(x1,y1),A2(x2,y2),A3(x3,y3)為雙曲線上的三點,且x1<0<x2<x3,請直接寫出y1,y2,y3的大小關系;
(3)觀察圖象,請直接寫出不等式kx+b<![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠ACB=90°,點D、E分別在AB、AC上,且CE=BC,連接CD,將線段CD繞點C按順時針方向旋轉90°后得到CF,連接EF.
(1)求證:△BDC≌△EFC;
(2)若EF∥CD,求證:∠BDC=90°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A、B是兩個工廠,L1、L2是兩條公路,現要在這一地區建一加油站,要求加油站到A、B兩廠的路程相等,且到兩條路的距離相等,請用尺規作圖找出符合條件的點P.
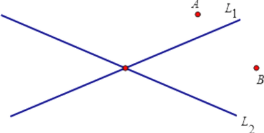
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A城氣象臺測得臺風中心在A城正西方向240km的O處,以每小時30km的速度向南偏東60°的OB方向移動,距臺風中心150km的范圍內是受臺風影響的區域.
(1)A城是否受到這次臺風的影響?為什么?
(2)若A城受到臺風的影響,求出受臺風影響的時間有多長?
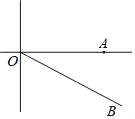
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com