
【題目】已知二次函數![]() .
.
(1)在給定的直角坐標系中,畫出這個函數的圖象;
(2)根據圖象,寫出當![]() 時,
時,![]() 的取值范圍;
的取值范圍;
(3)若將此圖象沿![]() 軸向左平移3個單位,向下移動2個單位,請寫出平移后圖象所對應的函數表達式.
軸向左平移3個單位,向下移動2個單位,請寫出平移后圖象所對應的函數表達式.
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 和
和![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
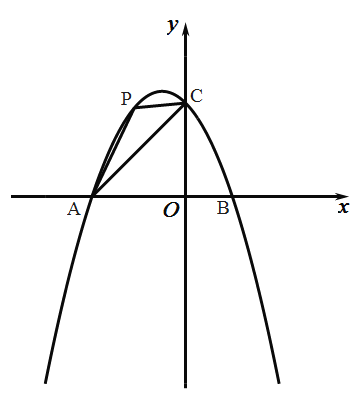
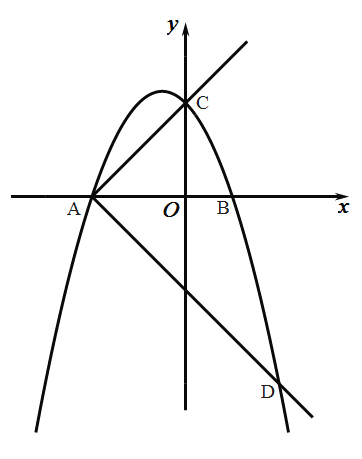
(1)求拋物線的表達式;
(2)點![]() 是拋物線上第二象限內的點,連接
是拋物線上第二象限內的點,連接![]() ,設
,設![]() 的面積為
的面積為![]() ,當
,當![]() 取最大值時,求點
取最大值時,求點![]() 的坐標;
的坐標;
(3)作射線![]() ,將射線
,將射線![]() 繞
繞![]() 點順時針旋轉
點順時針旋轉![]() 交拋物線于另一點
交拋物線于另一點![]() ,在射線
,在射線![]() 上是否存在一點
上是否存在一點![]() ,使
,使![]() 的周長最小.若存在,求出
的周長最小.若存在,求出![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
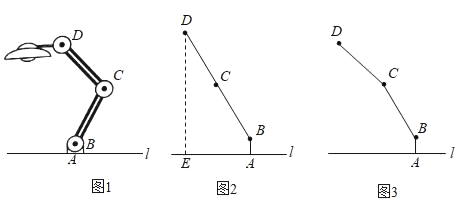
【題目】如圖1為放置在水平桌面l上的臺燈,底座的高AB為5cm,長度均為20cm的連桿BC、CD與AB始終在同一平面上.
(1)轉動連桿BC,CD,使∠BCD成平角,∠ABC=150°,如圖2,求連桿端點D離桌面l的高度DE.
(2)將(1)中的連桿CD再繞點C逆時針旋轉,經試驗后發現,如圖3,當∠BCD=150°時臺燈光線最佳.求此時連桿端點D離桌面l的高度比原來降低了多少厘米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為住宅區內的兩幢樓,它們的高AB=CD=30m,兩樓之間的距離AC=24m,現需了解甲樓對乙樓的采光的影響情況,當太陽光與水平線的夾角為30°時,求甲樓的影子在乙樓上有多高?(精確到0.1m,![]() ≈1.41,
≈1.41,![]() ≈1.73)?
≈1.73)?

查看答案和解析>>
科目:初中數學 來源: 題型:
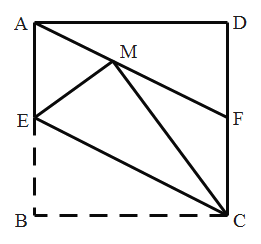
【題目】如圖,在正方形![]() 中,
中,![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 折疊,使點
折疊,使點![]() 落在點
落在點![]() 處,
處,![]() 的延長線與
的延長線與![]() 邊交于點
邊交于點![]() .下列四個結論:①
.下列四個結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() S正方形ABCD,其中正確結論的個數為( )
S正方形ABCD,其中正確結論的個數為( )
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】等邊![]() 的邊長為
的邊長為![]() ,等邊
,等邊![]() 的邊長為
的邊長為![]() ,把
,把![]() 放在
放在![]() 中,使
中,使![]() 與
與![]() 重合,點
重合,點![]() 在
在![]() 邊上,如圖所示,此時點
邊上,如圖所示,此時點![]() 是
是![]() 中點,在
中點,在![]() 內部將
內部將![]() 按下列方式旋轉:繞點
按下列方式旋轉:繞點![]() 順時針旋轉,使點
順時針旋轉,使點![]() 與點
與點![]() 重合,完成第
重合,完成第![]() 次操作,此時點
次操作,此時點![]() 是
是![]() 中點,
中點,![]() 旋轉了__________
旋轉了__________![]() ;再繞點
;再繞點![]() 順時針旋轉,使點
順時針旋轉,使點![]() 與點
與點![]() 重合,完成第
重合,完成第![]() 次操作;……這樣依次繞
次操作;……這樣依次繞![]() 的某個頂點連續旋轉下去,第
的某個頂點連續旋轉下去,第![]() 次操作完成時,
次操作完成時,![]() _____________.
_____________.
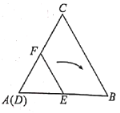
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知某個二次函數的圖象經過點A(1,2),B(2,﹣1),C(4,﹣1),且該二次函數的最小值是﹣2.

(1)請在圖中描出該函數圖象上另外的兩個點,并畫出圖象;
(2)求出該二次函數的解析.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:我們知道,四邊形的一條對角線把這個四邊形分成了兩個三角形,如果這兩個三角形相似(不全等),我們就把這條對角線叫做這個四邊形的“相似對角線”.
理解:(1)如圖1,已知Rt△ABC在正方形網格中,請你只用無刻度的直尺在網格中找到一點D,使四邊形ABCD是以AC為“相似對角線”的四邊形(保留畫圖痕跡,找出3個即可);
(2)如圖2,在四邊形ABCD中,∠ABC=80°,∠ADC=140°,對角線BD平分∠ABC.求證:BD是四邊形ABCD的“相似對角線”.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com