【題目】如圖，圓內接四邊形ABCD的BA，CD的延長線交于P，AC，BD交于E，則圖中相似三角形有( )
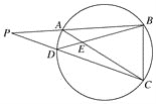
A. 2對 B. 3對 C. 4對 D. 5對
新課標階梯閱讀訓練系列答案科目：初中數學 來源： 題型：
【題目】截長補短法，是初中幾何題中一種添加輔助線的方法，也是把幾何題化難為易的一種策略．截長就是在長邊上截取一條線段與某一短邊相等，補短就是通過延長或旋轉等方式使兩條短邊拼合到一起，從而解決問題．
（1）如圖1，△ABC是等邊三角形，點D是邊BC下方一點，∠BDC＝120°，探索線段DA、DB、DC之間的數量關系．
解題思路：延長DC到點E，使CE＝BD，根據∠BAC+∠BDC＝180°，可證∠ABD＝∠ACE，易證△ABD≌△ACE，得出△ADE是等邊三角形，所以AD＝DE，從而解決問題．
根據上述解題思路，三條線段DA、DB、DC之間的等量關系是；（直接寫出結果）
（2）如圖2，Rt△ABC中，∠BAC＝90°，AB＝AC．點D是邊BC下方一點，∠BDC＝90°，探索三條線段DA、DB、DC之間的等量關系，并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
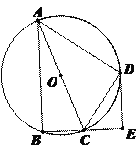
【題目】如圖，四邊形ABCD是⊙O的內接四邊形， 
，AC為直徑， DE⊥BC，垂足為E．
（1）求證：CD平分∠ACE；
（2）若AC＝9，CE＝3，求CD的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，正方形OABC的邊長為4，頂點A，C分別在x軸、y軸的正半軸上，拋物線y＝－
x2＋bx＋c經過點B，C兩點，點D為拋物線的頂點，連接AC，BD，CD.
(1)求此拋物線的解析式；
(2)求此拋物線頂點D的坐標和四邊形ABDC的面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，是由8個大小相同的小正方體組合成的簡單幾何體．
（1）該幾何體的主視圖如圖所示，請在下面方格紙中分別畫出它的左視圖和俯視圖；（邊框線加粗畫出，并涂上陰影）
（2）如果在這個幾何體上再添加一些相同的小正方體，并保持這個幾何體的俯視圖和主視圖不變，那么請在下列網格圖中畫出添加小正方體后所得幾何體所有可能的左視圖．
查看答案和解析>>
科目：初中數學 來源： 題型：
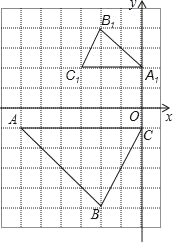
【題目】如圖，△ABC與△A1B1C1是位似圖形．
（1）在網格上建立平面直角坐標系，使得點A的坐標為（﹣6，﹣1），點C1的坐標為（﹣3，2），則點B的坐標為 ；
（2）以點A為位似中心，在網格圖中作△AB2C2，使△AB2C2和△ABC位似，且位似比為1：2；
（3）在圖上標出△ABC與△A1B1C1的位似中心P，并寫出點P的坐標為 ，計算四邊形ABCP的周長為 ．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，直線l1：y＝﹣
x與反比例函數y＝
的圖象交于A，B兩點（點A在點B左側），已知A點的縱坐標是2；
（1）求反比例函數的表達式；
（2）根據圖象直接寫出﹣x＞的解集；
（3）將直線l1：y＝- x沿y向上平移后的直線l2與反比例函數y＝在第二象限內交于點C，如果△ABC的面積為30，求平移后的直線l2的函數表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
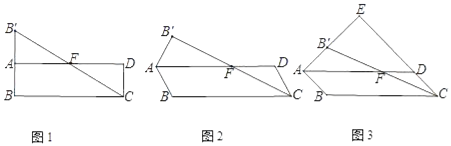
【題目】在ABCD中，點B關于AD的對稱點為B′，連接AB′，CB′，CB′交AD于F點．
（1）如圖1，∠ABC=90°，求證：F為CB′的中點；
（2）小宇通過觀察、實驗、提出猜想：如圖2，在點B繞點A旋轉的過程中，點F始終為CB′的中點．小宇把這個猜想與同學們進行交流，通過討論，形成了證明該猜想的幾種想法：
想法1：過點B′作B′G∥CD交AD于G點，只需證三角形全等；
想法2：連接BB′交AD于H點，只需證H為BB′的中點；
想法3：連接BB′，BF，只需證∠B′BC=90°．
…
請你參考上面的想法，證明F為CB′的中點．（一種方法即可）
（3）如圖3，當∠ABC=135°時，AB′，CD的延長線相交于點E，求
的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
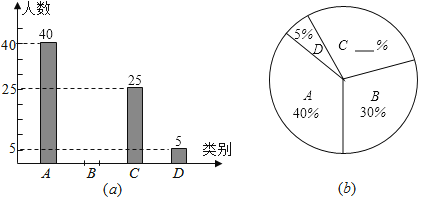
【題目】為了了解某區2018年初中畢業生畢業后的去向，某區教育部門對部分初三學生進行了抽樣調查，就初三學生的四種去向（A，讀普通高中；B，讀職業高中；C，直接進入社會就業；D，其它）進行數據統計，并繪制了兩幅不完整的統計圖（a）、（b）．請問：
（1）此次共調查了多少名初中畢業生？
（2）將兩幅統計圖中不完整的部分補充完整；
（3）若某區2018年初三畢業生共有3500人，請估計2019年初三畢業生中讀普通高中的學生人數．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
