
【題目】推理填空:
如圖,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代換)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代換)
∴AB∥CD ( )

 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案科目:初中數學 來源: 題型:
【題目】在□ABCD中,點E在CD上,點F在AB上,連接AE、CF、DF、BE,∠DAE=∠BCF.
(1)如圖1,求證:四邊形DFBE是平行四邊形;
(2)如圖2,若E是CD的中點,連接GH,在不添加任何輔助線的情況下,請直接寫出圖2中以GH為邊或以GH為對角線的所有平行四邊形.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,等腰△ABC中,AB=AC,∠BAC=30°,AB邊上的中垂線DE分別交AB,AC于點D、E,∠BAC的平分線交DE于點F.連接BF、CF、BE.
(1)求證:△BCF為等邊三角形;
(2)猜想EF、EB、EC三條線段的關系,并說明理由;
(3)如圖2,在BE的延長線上取一點M,連接AM,使AM=AB,連接MC并延長交AF的延長線于點M.求證:AN=MC.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答題
(1)如圖1,在正方形ABCD中,點E,F分別在BC,CD上,AE⊥BF于點M,求證:AE=BF; 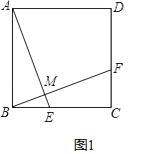
(2)如圖2,將 (1)中的正方形ABCD改為矩形ABCD,AB=2,BC=3,AE⊥BF于點M,探究AE與BF的數量關系,并證明你的結論. 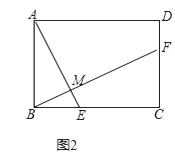
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】心理學家研究發現,一般情況下,一節課![]() 分鐘中,學生的注意力隨教師講課的變化而變化.開始上課時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為 理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指標數
分鐘中,學生的注意力隨教師講課的變化而變化.開始上課時,學生的注意力逐步增強,中間有一段時間學生的注意力保持較為 理想的穩定狀態,隨后學生的注意力開始分散.經過實驗分析可知,學生的注意力指標數![]() 隨時間
隨時間![]() (分鐘)的變化規律如圖所示(其中
(分鐘)的變化規律如圖所示(其中![]() 都為線段)
都為線段)
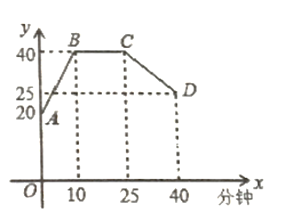
(1)分別求出線段![]() 和
和![]() 的函數解析式;
的函數解析式;
(2)開始上課后第![]() 分鐘時與第
分鐘時與第![]() 分鐘時相比較,何時學生的注意力更集中?
分鐘時相比較,何時學生的注意力更集中?
(3)一道數學競賽題,需要講![]() 分鐘,為了效果較好,要求學生的注意力指標數最低達到
分鐘,為了效果較好,要求學生的注意力指標數最低達到![]() 那么經過適當安排,老師能否在學生注意力達到所需的狀態下講解完這道題目?
那么經過適當安排,老師能否在學生注意力達到所需的狀態下講解完這道題目?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)2﹣2+(![]() )0+(﹣0.2)2014×52014
)0+(﹣0.2)2014×52014
(2)(2a3b)3(﹣8ab2)÷(﹣4a4b3)
(3)(2a+1)2﹣(2a+1)(﹣1+2a)
(4)20192﹣2018×2020(運用整式乘法公式進行計算)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,CD⊥AB,垂足為D,點E在BC上,EF⊥AB,垂足為F.

(1)CD與EF平行嗎?為什么?
(2)如果∠1=∠2,且∠3=120°,求∠ACB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC和△DEC中,AB=DE.若添加條件后使得△ABC≌△DEC,則在下列條件中,不能添加的是( )

A. BC=EC,∠B=∠E B. BC=EC,AC=DC
C. ∠B=∠E,∠A=∠D D. BC=EC,∠A=∠D
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“九宮圖”傳說是遠古時代洛河中的一個神龜背上的圖案,故又稱“龜背圖”,中國古代數學史上經常研究這一神話。
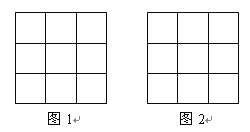
⑴現有1,2,3,4,5,6,7,8,9共九個數字,請將它們分別填入圖1的九個方格中,使得每行的三個數、每列的三個數、斜對角的三個數之和都等于15.
⑵通過研究問題⑴,利用你發現的規律,將3,5,-7,1,7,-3,9,-5,-1
這九個數字分別填入圖2的九個方格中,使得橫、豎、斜對角的所有三個數的和都相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com