
【題目】![]() 兩地相距120km,甲、乙兩人從兩地出發相向而行,甲先出發.圖中
兩地相距120km,甲、乙兩人從兩地出發相向而行,甲先出發.圖中![]() 表示兩人離
表示兩人離![]() 地的距離
地的距離![]() (km)與時間 (h)的關系,結合圖像回答下列問題:
(km)與時間 (h)的關系,結合圖像回答下列問題:
(1)表示乙離開![]() 地的距離與時間關系的圖像是 (填
地的距離與時間關系的圖像是 (填![]() 或
或![]() );
);
甲的速度是 km/h,乙的速度是 km/h.
(2)何時兩人在途中相遇?
(3)甲出發后多少時間兩人恰好相距10km?

【答案】(1)![]() ,30,20;(2)2.8h;(3)2.6h或3h.
,30,20;(2)2.8h;(3)2.6h或3h.
【解析】
(1)甲先出發,可判定乙的圖像是![]() ;分別根據圖像上的距離和時間可求得甲乙的速度;
;分別根據圖像上的距離和時間可求得甲乙的速度;
(2)首先根據圖像的性質,設直線解析式,然后將點代入得出直線解析式,聯立方程,解得即為相遇時間;
(3)分類討論:①相遇前:![]() ,
,![]() ;②相遇后:
;②相遇后:![]() ,
,![]() .
.
(1)根據題意,得
甲先出發,乙后出發,可判定表示乙離開![]() 地的距離與時間關系的圖像是
地的距離與時間關系的圖像是![]() ;
;
則![]() 表示甲離開
表示甲離開![]() 地的距離與時間關系的圖像;
地的距離與時間關系的圖像;
甲的速度是![]()
乙的速度是![]()
(2)由圖可知,![]() 過點(0,120),(4,0)
過點(0,120),(4,0)
![]() 過點(1,0),(7,120)
過點(1,0),(7,120)
則設![]() 解析式為
解析式為![]()
![]()
![]() 解析式為
解析式為![]()
設![]() 的解析式為
的解析式為![]()
![]() 解得
解得![]()
![]() 解析式為
解析式為![]()
聯立兩直線得
解得![]()
∴兩人在甲出發2.8h后在途中相遇.
(3)由題意得,
相遇前:![]()
解得![]()
相遇后:![]()
解得![]()
∴甲出發后2.6h或3h兩人恰好相距10km.


 應用題點撥系列答案
應用題點撥系列答案 狀元及第系列答案
狀元及第系列答案 同步奧數系列答案
同步奧數系列答案科目:初中數學 來源: 題型:
【題目】 (1)閱讀理解:
我們知道,只用直尺和圓規不能解決的三個經典的希臘問題之一是三等分任意角,但是這個任務可以借助如圖所示的一邊上有刻度的勾尺完成,勾尺的直角頂點為P,“寬臂”的寬度=PQ= QR = RS,(這個條件很重要哦!)勾 尺的一邊 MN 滿足M, N, Q三點共線(所以PQ ⊥ MN).
下面以三等分∠ABC為例說明利用勾尺三等分銳角的過程:
第一步:畫直線DE使DE //BC,且這兩條平行線的距離等于PQ;
第二步:移動勾尺到合適位置,使其頂點P落在DE上,使勾尺的MN邊經過點B,同時讓點R落在∠ABC的BA邊上;
第三步:標記此時點Q和點P所在位置,作射線BQ和射線BP:
請完成第三步操作,圖中∠ABC的三等分線是射線 、 .
(2)在(1)的條件下補全三等分∠ABC的主要證明過程:
∵ ,BQ ⊥ PR,
∴BP= BR.(線段垂直平分線上的點與這條線段兩個端點的距離相等)
∴∠RBQ=∠PBQ,
∵PT⊥BC,PQ⊥BQ,PT=PQ,
∴∠ = ∠ . (角的內部到角的兩邊距離相等的點在角的平分線上)
∴∠ = = ∠ = ∠
(3)在(1)的條件下探究:
∠ABS=![]() ∠ABC是否成立?如果成立,請說明理由;如果不成立,請在下圖中∠ABC外部畫出∠ABV =
∠ABC是否成立?如果成立,請說明理由;如果不成立,請在下圖中∠ABC外部畫出∠ABV =![]() ∠ABC(無需寫畫法,保留畫圖痕跡即可)
∠ABC(無需寫畫法,保留畫圖痕跡即可)

查看答案和解析>>
科目:初中數學 來源: 題型:
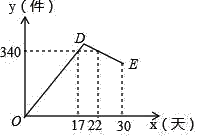
【題目】某公司開發出一款新的節能產品,該產品的成本價為6元件,該產品在正式投放市場前通過代銷點進行了為期30天的試銷售,售價為8元/件,工作人員對銷售情況進行了跟蹤記錄,并將記錄情況繪成如圖所示的圖象,圖中的折線ODE表示日銷售量y(件)與銷售時間x(天)之間的函數關系,已知線段DE表示的函數關系中,時間每增加1天,日銷售量減少5件.
(1)第24天的日銷售量是 件,日銷售利潤是 元.
(2)求線段DE所對應的函數關系式.(不要求寫出自變量的取值范圍)
(3)通過計算說明試銷售期間第幾天的日銷售量最大?最大日銷售量是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,如圖:在平面直角坐標系中,O為坐標原點,四邊形OABC是長方形,點A、C、D的坐標分別為A(9,0)、C(0,4),D(5,0),點P從點O出發,以每秒1個單位長度的速度沿O→C→B→A運動,點P的運動時間為t秒.
(1)當t=5時, OP長為____________;
(2)當點P在BC邊上時,OP+PD有最小值嗎?如果有,請算出該最小值,如果沒有,請說明理由;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場購進甲、乙兩種商品,甲種商品共用了![]() 元,乙種商品共用了
元,乙種商品共用了![]() 元.已知乙種商品每件進價比甲種商品每件進價多
元.已知乙種商品每件進價比甲種商品每件進價多![]() 元,且購進的甲、乙兩種商品件數相同.
元,且購進的甲、乙兩種商品件數相同.
![]() 求甲、乙兩種商品的每件進價;
求甲、乙兩種商品的每件進價;
![]() 該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為
該商場將購進的甲、乙兩種商品進行銷售,甲種商品的銷售單價為![]() 元,乙種商品的銷售單價為
元,乙種商品的銷售單價為![]() 元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的九折銷售;乙種商品銷售單價保持不變.要使兩種商品全部售完后共獲利不少于
元,銷售過程中發現甲種商品銷量不好,商場決定:甲種商品銷售一定數量后,將剩余的甲種商品按原銷售單價的九折銷售;乙種商品銷售單價保持不變.要使兩種商品全部售完后共獲利不少于![]() 元,問甲種商品按原銷售單價至少銷售多少件?
元,問甲種商品按原銷售單價至少銷售多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平面直角坐標系中,△ABC的三個頂點坐標分別為A(-2,4), B(-3,-2),C(1,2).
(1)畫出△ABC關于x軸對稱的△A1B1C1,寫出點A1、B1、C1的坐標.
(2)在y軸上找一個點P,使△ABP的周長最小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,∠ABC=∠ACB,把這個三角形折疊,使得點B與點A重合,折痕分別交直線AB,AC于點M,N,若∠ANM=50°,則∠B的度數為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,已知A、B、C、D四點的坐標依次為(0,0)、(6,0)(8,6)、(2,6),若一次函數y=mx﹣6m的圖象將四邊形ABCD的面積分成1:3兩部分,則m的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
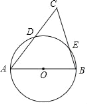
【題目】如圖,AB是⊙O的直徑,C是⊙O外一點,AC,BC分別與⊙O相交于D.
(1)在圖中作出△ABC的邊AB上的高CH.(要求:①僅用無刻度真尺,且不能用直尺中的直角;②保留必要的作圖痕跡)
(2)連接DE,若![]() ,則∠C的度數是 .
,則∠C的度數是 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com