
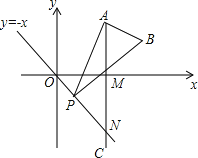
【題目】如圖,已知點A是第一象限內(nèi)橫坐標為![]() 的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是_____.
的一個定點,AC⊥x軸于點M,交直線y=﹣x于點N.若點P是線段ON上的一個動點,∠APB=30°,BA⊥PA,則點P在線段ON上運動時,A點不變,B點隨之運動.求當點P從點O運動到點N時,點B運動的路徑長是_____.
【答案】![]() .
.
【解析】
首先,需要證明線段B1B2就是點B運動的路徑(或軌跡),如圖1所示.利用相似三角形可以證明;其次,證明△APN∽△AB1B2,列比例式可得B1B2的長.
解:如圖1所示,當點P運動至ON上的任一點時,設其對應的點B為Bi,連接AP,ABi,BBi,
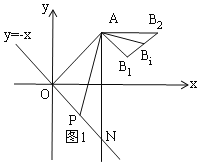
∵AO⊥AB1,AP⊥ABi,
∴∠OAP=∠B1ABi,
又∵AB1=AOtan30°,ABi=APtan30°,
∴AB1:AO=ABi:AP,
∴△AB1Bi∽△AOP,
∴∠B1Bi=∠AOP.
同理得△AB1B2∽△AON,
∴∠AB1B2=∠AOP,
∴∠AB1Bi=∠AB1B2,
∴點Bi在線段B1B2上,即線段B1B2就是點B運動的路徑(或軌跡).
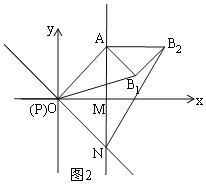
由圖形2可知:Rt△APB1中,∠APB1=30°,
∴![]()
Rt△AB2N中,∠ANB2=30°,
∴![]()
∴![]()
∵∠PAB1=∠NAB2=90°,
∴∠PAN=∠B1AB2,
∴△APN∽△AB1B2,
∴![]() ,
,
∵ON:y=﹣x,
∴△OMN是等腰直角三角形,
∴OM=MN=![]() ,
,
∴PN=![]() ,
,
∴B1B2=![]() ,
,
綜上所述,點B運動的路徑(或軌跡)是線段B1B2,其長度為![]() .
.
故答案為:![]() .
.


 新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案
新課標快樂提優(yōu)暑假作業(yè)陜西旅游出版社系列答案科目:初中數(shù)學 來源: 題型:
【題目】如圖,四邊形![]() 內(nèi)接于
內(nèi)接于![]() ,對角線
,對角線![]() 為
為![]() 的直徑,過點
的直徑,過點![]() 作AC的垂線交AD的延長線于點E,點F為CE的中點,連接DB,DC,DF.
作AC的垂線交AD的延長線于點E,點F為CE的中點,連接DB,DC,DF.
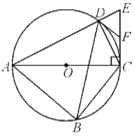
(1)求證:DF是![]() 的切線;
的切線;
(2)若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】《九章算術(shù)》是中國古代的數(shù)學專著,它的出現(xiàn)標志中國古代數(shù)學形成了完整的體系.其中有一個問題:“今有二馬、一牛價過-萬,如半馬之價:一馬、二牛價不滿一萬,如半牛之價.問牛、馬價各幾何?”其大意為:現(xiàn)有兩匹馬加一頭牛的價錢超過一萬,超過的部分正好是半匹馬的價錢:一匹馬加上兩頭牛的價錢則不到一萬,不足的部分正好是半頭牛的價錢.問一頭牛、一匹馬各多少錢?設一匹馬值![]() 錢、一頭牛值
錢、一頭牛值![]() 錢,則符合題意的方程組為( )
錢,則符合題意的方程組為( )
A. B.
B.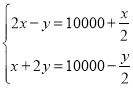
C.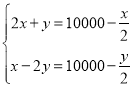 D.
D.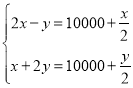
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某微商銷售的某商品每袋成本20元,設銷售價格為x(單位:元/袋),該微商發(fā)現(xiàn)銷售量y與銷售價格x之間的關(guān)系如表:
銷售價格x(元/袋) | 25 | 30 | 35 | 40 |
銷售件數(shù)y | 275 | 250 | 225 | 200 |
(1)求y關(guān)于x的函數(shù)表達式;
(2)根據(jù)物價部門的規(guī)定,商品的利潤率不能超過100%,該微商應該如何定價,才能使獲得的利潤最大,最大利潤是多少?
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
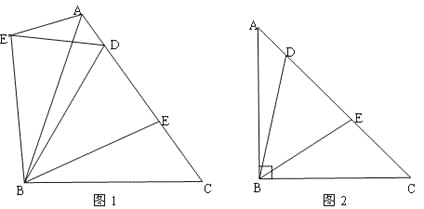
【題目】(1)如圖1,在△ABC中,BA=BC,D,E是AC邊上的兩點,且滿足∠DBE=![]() ∠ABC(0°<∠CBE<
∠ABC(0°<∠CBE<![]() ∠ABC).以點B為旋轉(zhuǎn)中心,將△BEC按逆時針方向旋轉(zhuǎn)∠ABC,得到△BE′A(點C與點A重合,點E到點E′處),連接DE′.求證:DE′=DE;
∠ABC).以點B為旋轉(zhuǎn)中心,將△BEC按逆時針方向旋轉(zhuǎn)∠ABC,得到△BE′A(點C與點A重合,點E到點E′處),連接DE′.求證:DE′=DE;
(2)如圖2,在△ABC中,BA=BC,∠ABC=90°,D,E是AC邊上的兩點,
且滿足∠DBE=![]() ∠ABC(0°<∠CBE<45°) .求證:DE2=AD2+EC2.
∠ABC(0°<∠CBE<45°) .求證:DE2=AD2+EC2.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
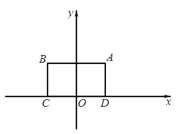
【題目】對于⊙P及一個矩形給出如下定義:如果⊙P上存在到此矩形四個頂點距離都相等的點,那么稱⊙P是該矩形的“等距圓”.如圖,在平面直角坐標系xOy中,矩形ABCD的頂點A的坐標為(![]() ,
,![]() ),頂點C、D在x軸上,且OC=OD.
),頂點C、D在x軸上,且OC=OD.
(1)當⊙P的半徑為4時,
①在P1(![]() ,
,![]() ),P2(
),P2(![]() ,
,![]() ),P3(
),P3(![]() ,
,![]() )中可以成為矩形ABCD的“等距圓”的圓心的是 ;
)中可以成為矩形ABCD的“等距圓”的圓心的是 ;
②如果點P在直線![]() 上,且⊙P是矩形ABCD的“等距圓”,求點P的坐標;
上,且⊙P是矩形ABCD的“等距圓”,求點P的坐標;
(2)已知點P在![]() 軸上,且⊙P是矩形ABCD的“等距圓”,如果⊙P與直線AD沒有公共點,直接寫出點P的縱坐標m的取值范圍.
軸上,且⊙P是矩形ABCD的“等距圓”,如果⊙P與直線AD沒有公共點,直接寫出點P的縱坐標m的取值范圍.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() ,直線
,直線![]() 與y軸交于點A,與雙曲線
與y軸交于點A,與雙曲線![]() 交于點
交于點![]() .
.
(1)求點B的坐標及k的值;
(2)將直線AB平移,使它與x軸交于點C,與y軸交于點D,若![]() 的面積為6,求直線CD的表達式.
的面積為6,求直線CD的表達式.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖所示,以Rt△ABC的斜邊BC為一邊在△ABC的同側(cè)作正方形BCEF,設正方形的中心為O,連接AO,如果AB=4,AO=6![]() ,那么AC=_____.
,那么AC=_____.

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】同學們參加綜合實踐活動時,看到木工師傅用“三弧法”在板材邊角處作直角,其作法是:如圖:
(1)作線段AB,分別以點A,B為圓心,AB長為半徑作弧,兩弧交于點C;
(2)以點C為圓心,仍以AB長為半徑作弧交AC的延長線于點D;
(3)連接BD,BC.
根據(jù)以上作圖過程及所作圖形,下列結(jié)論中錯誤的是( )

A.∠ABD=90°B.CA=CB=CDC.sinA=![]() D.cosD=
D.cosD=![]()
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com