
【題目】如圖1,已知拋物線![]() 經過點
經過點![]() (9,10),交
(9,10),交![]() 軸于點
軸于點![]() ,直線
,直線![]() ∥
∥![]() 軸,點
軸,點![]() 是直線
是直線![]() 下方拋物線上的動點.
下方拋物線上的動點.
(1)直接寫出拋物線的解析式為 ,點![]() 的坐標為 、
的坐標為 、![]() 的坐標為 _;
的坐標為 _;
(2)過點![]() 且與
且與![]() 軸平行的直線
軸平行的直線![]() 與直線
與直線![]() 、
、![]() 分別交于點
分別交于點![]() 、
、![]() ,當四邊形
,當四邊形![]() 的面積最大時,求
的面積最大時,求![]() 點的坐標;
點的坐標;
(3)如圖2,當點![]() 為拋物線的頂點時,在直線
為拋物線的頂點時,在直線![]() 上是否存在點
上是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,若存在,求出點
相似,若存在,求出點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.



【答案】(1)![]() ,B(0,1),C(6,1);(2)P(
,B(0,1),C(6,1);(2)P(![]() );(3)Q(-3,1),或(4,1).
);(3)Q(-3,1),或(4,1).
【解析】分析:(1)由點A坐標可得拋物線解析式,求出x=0時y的值即可知點B坐標,再根據拋物線對稱性得出點C坐標;
(2)設點P(m, ![]() m-2m+1),表示出PD=
m-2m+1),表示出PD=![]() m+3m,再用S四邊形PBDC=S△BDC+S△APC=
m+3m,再用S四邊形PBDC=S△BDC+S△APC=![]() BC×PD,建立函數關系式,求出極值即可;
BC×PD,建立函數關系式,求出極值即可;
(3)先判斷出PE=CE,再得到∠PCE=∠DBE,以C、P、Q為頂點的三角形與△ABC相似,分兩種情況計算即可.
本題解析:
(1)將點A(9,10)代入得:81a18+1=10,
解得:a=![]() ,
,
∴拋物線解析式為y=![]() x2x+1,
x2x+1,
當x=0時,y=1,即點B(0,1),
∵拋物線對稱軸為x=3,
∴點B關于對稱軸的對稱點C坐標為(6,1),
故答案為:y=![]() x2x+1,(0,1),(6,1);
x2x+1,(0,1),(6,1);
(2)如圖2,
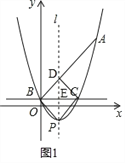
設直線AB的解析式為y=kx+b,
將A(9,10)、B(0,1)代入得: ![]() ,
,
解得: ![]() ,
,
∴直線AB的解析式為y=x+1,
設點P(m, ![]() m2m+1)
m2m+1)
∴D(m,m+1)
∴PD=m+1(![]() m2m+1)=
m2m+1)= ![]() m+3m,
m+3m,
∵BC⊥PD,BC=6,
∴S四邊形PBDC=S△BDC+S△APC=![]() BC×DE+12BC×PE=
BC×DE+12BC×PE=![]() BC(DE+PE)=
BC(DE+PE)= ![]() BC×PD=
BC×PD=![]() ×6×(
×6×(![]() m+3m)=m+9m=(m
m+3m)=m+9m=(m![]() )+
)+![]() ,
,
∵0<m<6,
∴當m=![]() 時,四邊形PBDC的面積取得最大值
時,四邊形PBDC的面積取得最大值![]() ,
,
此時點P的坐標為(![]() ,
,![]() ;
;
(3)如圖2,
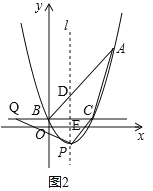
∵y=![]() x2x+1=
x2x+1=![]() (x3)2,
(x3)2,
∴P(3,2),
∴PE=![]() =3,CE=
=3,CE=![]() =3,
=3,
∴PE=CE,
∴∠PCE=45°
同理可得:∠DBE=45°,
∴∠PCE=∠DBE,
∴在直線AC上存在滿足條件的Q,
設Q(t,1)且AB=9![]() ,BC=6,CP=3
,BC=6,CP=3![]() ,
,
∵以C. P、Q為頂點的三角形與△ABC相似,
①當△CPQ∽△BAC時,
∴![]() ,
,
∴![]() ,
,
∴t=4,
∴Q(4,1)
②當△CPQ∽△BCA時,
∴![]() ,
,
∴![]() ,
,
∴t=3,
∴Q(3,1),
綜上,點Q的坐標為(4,1)或(3,1).


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,將矩形ABCO放在直角坐標系中,其中頂點B的坐標為(10, 8),E是BC邊上一點將△ABE沿AE折疊,點B剛好與OC邊上點D重合,過點E的反比例函數y=![]() 的圖象與邊AB交于點F, 則線段AF的長為( )
的圖象與邊AB交于點F, 則線段AF的長為( )

A. ![]() B. 2 C.
B. 2 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,方格紙中的每個小方格都是邊長為1個單位長度的正方形,△ABC的頂點均在格點上,在建立平面直角坐標系后,點C的坐標為(-2,-2).
(1)畫出△ABC以y軸為對稱軸的對稱圖形![]() ,并寫出點C1的坐標;
,并寫出點C1的坐標;
(2)以原點O為對稱中心,畫出![]() 關于原點O對稱的
關于原點O對稱的![]() 并寫出點C2的坐標;
并寫出點C2的坐標;
(3)以C2為旋轉中心,把![]() 順時針旋轉90°,得到△C2A3B3.
順時針旋轉90°,得到△C2A3B3.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形ABCD中,AB=1,BC=2,點E在AD上,點F在BC邊上,FE平分∠DFB.

(1)判斷△DEF的形狀,并說明理由;
(2)若點F是BC的中點,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.

(1)求證:四邊形AECD是菱形;
(2)若點E是AB的中點,試判斷△ABC的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D、E分別在邊AB、AC上,DE、BC的延長線相交于點F,且![]() .
.
(1)求證![]() ;
;
(2)當AB=12,AC=9,AE=8時,求BD的長與![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如果![]() +(n+6)2=0,求(m+n)2008+m3的值
+(n+6)2=0,求(m+n)2008+m3的值
(2)已知實數a,b,c,d,e,且ab互為倒數,c,d互為相反數,e的絕對值為2,求![]() ×ab+
×ab+![]() +e的值
+e的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國數學史上最先完成勾股定理證明的數學家是公元3世紀三國時期的趙爽,他為了證明勾股定理,創制了一副“弦圖”,后人稱其為“趙爽弦圖”(如圖1).圖2由弦圖變化得到,它是由八個全等的直角三角形拼接而成. 將圖中正方形MNKT,正方形EFGH,正方形ABCD的面積分別記為![]() ,
,![]() ,
,![]() . 若
. 若![]() , 則正方形EFGH的面積為_______.
, 則正方形EFGH的面積為_______.
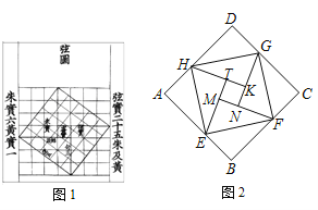
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com