
【題目】如圖1,點A、B在直線MN上(A在B的左側),點P是直線MN上方一點.若∠PAN=x°,∠PBN=y°,記< x,y >為P的雙角坐標.例如,若△PAB是等邊三角形,則點P的雙角坐標為< 60,120 >.
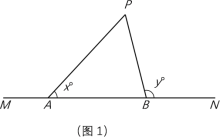

(1)如圖2,若AB=22 cm,P<26.6,58>,求△PAB的面積;
(參考數據:tan26.6°≈0.50,tan58°≈1.60.)
(2)在圖3中用直尺和圓規作出點P < x,y >,其中y=2x且y=x+30.(保留作圖痕跡)
![]()
【答案】(1)S△PAB=176 cm2;(2)見解析.
【解析】
(1)過P作PC⊥AB,垂足為C,則∠PCA=90°,利用三角函數求解即可;
(2)通過y=2x且y=x+30,得到x=30,y=60,可通過作等邊三角形的方法作出點P.
(1)解:過P作PC⊥AB,垂足為C,則∠PCA=90°.

在Rt△PBC中,∠PBC=58°,
∵ tan58°=![]() ,
,
∴ BC=![]() ,
,
在Rt△PAC中,∠PAC=26.6°,
∵ tan26.6°=![]() ,
,
∴ AC=![]() ,
,
∵ AB=AC-BC,
∴ ![]() -
-![]() =22.
=22.
解得PC≈16 cm.
∴ S△PAB=![]() ×22×16=176 cm2.
×22×16=176 cm2.
(2)∵y=2x且y=x+30,
∴2x=x+30,
即x=30,y=60,
以B為圓心AB長為半徑畫弧,再以A為圓心AB長為半徑畫弧交之前的弧于點O,然后以O為圓心AB長為半徑畫弧,即可得到點P,
如圖,點P即為所求.



科目:初中數學 來源: 題型:
【題目】港口 A、B、C 依次在同一條直線上,甲、乙兩艘船同時分別從 A、B兩港出發,勻速駛向 C 港,甲、乙兩船與 B 港的距離 y(海里)與行駛時間 x 時)之間的函數關系如圖所示,則下列說法錯誤的是( )
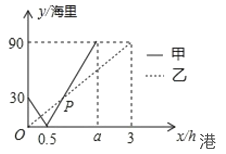
A.甲船平均速度為 60 海里/時B.乙船平均速度為 30 海里/時
C.甲、乙兩船在途中相遇兩次D.A、C 兩港之間的距離為 120 海里
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在![]() 中,
中,![]() ,
,![]() 是邊
是邊![]() 上的一點(不與點
上的一點(不與點![]() 重合),邊
重合),邊![]() 上點
上點![]() 在點
在點![]() 的右邊且
的右邊且![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為
的對稱點為![]() ,連接
,連接![]() .
.
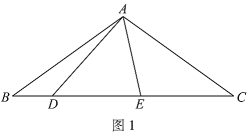
(1)如圖1,
①依題意補全圖1;
②求證:![]() ;
;
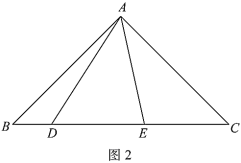
(2)如圖2,![]() ,用等式表示線段
,用等式表示線段![]() ,
,![]() ,
,![]() 之間的數量關系,并證明.
之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一家經營打印耗材的門店經銷各種打印耗材,其中某一品牌硒鼓的進價為![]() 元/個,售價為
元/個,售價為![]() 元/個(
元/個(![]() ).下面是門店在銷售一段時間后銷售情況的反饋:
).下面是門店在銷售一段時間后銷售情況的反饋:
①若每個硒鼓按定價30元的8折出售,可獲![]() 的利潤;
的利潤;
②如果硒鼓按30元/個的價格出售,每月可售出500個,在此基礎上,售價每增加5元,月銷售量就減少50個.
(1)求![]() 的值,并寫出該品牌硒鼓每月的銷售量
的值,并寫出該品牌硒鼓每月的銷售量![]() (個)與售價
(個)與售價![]() (元/個)之間的函數關系式,并注明自變量
(元/個)之間的函數關系式,并注明自變量![]() 的取值范圍;
的取值范圍;
(2)求該耗材店銷售這種硒鼓每月獲得的利潤![]() (元)與售價
(元)與售價![]() (元/個)之間的函數關系式,并求每月獲得的最大利潤;
(元/個)之間的函數關系式,并求每月獲得的最大利潤;
(3)在新冠肺炎流行期間,這種硒鼓的進價降低為![]() 元/個,售價為
元/個,售價為![]() 元/個(
元/個(![]() ).耗材店在2月份仍然按照銷售量與售價關系不變的方式銷售,并決定將當月銷售這種硒鼓獲得的利潤全部捐贈給火神山醫院,支援武漢抗擊新冠肺炎.若要使這個月銷售這種硒鼓獲得的利潤
).耗材店在2月份仍然按照銷售量與售價關系不變的方式銷售,并決定將當月銷售這種硒鼓獲得的利潤全部捐贈給火神山醫院,支援武漢抗擊新冠肺炎.若要使這個月銷售這種硒鼓獲得的利潤![]() (元)隨售價
(元)隨售價![]() (元/個)的增大而增大,請直接寫出
(元/個)的增大而增大,請直接寫出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是邊BC上的一個動點,以AD為直徑畫⊙O分別交AB、AC于點E、F,則弦EF長度的最小值為( )

A.![]() B.
B.![]() C.2
C.2![]() D.2
D.2![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() (
(![]() 是常數,
是常數,![]() )與
)與![]() 軸交于
軸交于![]() 兩點,頂點
兩點,頂點![]() 給出下列結論:①
給出下列結論:①![]() ;②若
;②若![]() 在拋物線上,則
在拋物線上,則![]() ;③關于
;③關于![]() 的方程
的方程![]() 有實數解,則
有實數解,則![]() ;④當
;④當![]() 時,
時,![]() 為等腰直角三角形,其中正確的結論是( )
為等腰直角三角形,其中正確的結論是( )
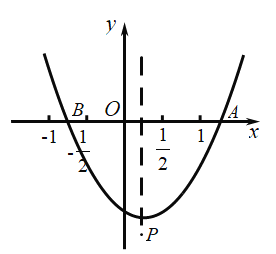
A.①②B.①③C.②③D.②④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線L:y=ax2+bx+c與x軸交于A、B(3,0)兩點(A在B的左側),與y軸交于點C(0,3),已知對稱軸x=1.
(1)求拋物線L的解析式;
(2)將拋物線L向下平移h個單位長度,使平移后所得拋物線的頂點落在△OBC內(包括△OBC的邊界),求h的取值范圍;
(3)設點P是拋物線L上任一點,點Q在直線l:x=﹣3上,△PBQ能否成為以點P為直角頂點的等腰直角三角形?若能,求出符合條件的點P的坐標;若不能,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2008年5月1日,目前世界上最長的跨海大橋——杭州灣跨海大橋通車了.通車后,蘇南A地到寧波港的路程比原來縮短了120千米.已知運輸車速度不變時,行駛時間將從原來的3時20分縮短到2時.
(1)求跨海大橋到寧波港的路程.
(2)若貨物運輸費用=A地經杭州灣包括運輸成本和時間成本,已知某車貨物從A地到寧波港的運輸成本是每千米1.8元,時間成本是每時28元,那么該車貨物從A地經杭州灣跨海大橋到寧波港的運輸費用是多少元?
(3)A地準備開辟寧波方向的外運路線,即貨物從A地經杭州灣跨海大橋到寧波港,再從寧波港運到B地.若有一批貨物(不超過10車)從A地按外運路線運到B地的運費需8320元,其中從A地經杭州灣跨海大橋到寧波港的每車運輸費用與(2)中相同,從寧波港到B地的海上運費對一批不超過10車的貨物計費方式是:一車800元,當貨物每增加1車時,每車的海上運費就減少20元,問這批貨物有幾車?
查看答案和解析>>
科目:初中數學 來源: 題型:
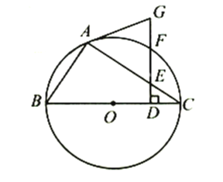
【題目】如圖,![]() 為⊙
為⊙![]() 的內接三角形,
的內接三角形,![]() 為⊙
為⊙![]() 的直徑,在線段
的直徑,在線段![]() 上取點
上取點![]() (不與端點重合),作
(不與端點重合),作![]() ,分別交
,分別交![]() 、圓周于
、圓周于![]() 、
、![]() ,連接
,連接![]() ,已知
,已知![]() .
.
(1)求證:![]() 為⊙
為⊙![]() 的切線;
的切線;
(2)已知![]() ,填空:
,填空:
①當![]() __________
__________![]() 時,四邊形
時,四邊形![]() 是菱形;
是菱形;
②若![]() ,當
,當![]() __________時,
__________時,![]() 為等腰直角三角形.
為等腰直角三角形.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com