
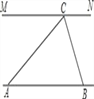
【題目】為解決江北學校學生上學過河難的問題,鄉政府決定修建一座橋,建橋過程中需測量河的寬度(即兩平行
河岸AB與MN之間的距離).在測量時,選定河對岸MN上的點C處為橋的一端,在河岸點A處,測得∠CAB=30°,
沿河岸AB前行30米后到達B處,在B處測得∠CBA=60°,請你根據以上測量數據求出河的寬度.(參考數據: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,結果保留整數)
≈1.73,結果保留整數)
 舉一反三單元同步過關卷系列答案
舉一反三單元同步過關卷系列答案科目:初中數學 來源: 題型:
【題目】定義:我們把對角線互相垂直的四邊形叫做和美四邊形,對角線交點稱為和美四邊形的中心.
(1)寫出一種你學過的和美四邊形_________;
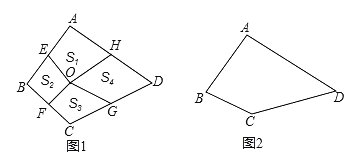
(2)如圖1,點O是和美四邊形ABCD的中心,E,F,G、H分別是邊AB,BC,CD,DA的中點,連接OE,OF,OG,OH,記四邊形AEOH,BEOF,CGOF,DHOG的面積為![]() ,用等式表示
,用等式表示![]() 的數量關系(無需說明理由).
的數量關系(無需說明理由).
(3)如圖2,四邊形ABCD是和美四邊形,若AB=3,BC=2,CD=4,求AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 是
是 ![]() 的中線,
的中線, ![]() 是線段
是線段 ![]() 上一點(不與點
上一點(不與點 ![]() 重合).
重合). ![]() 交
交 ![]() 于點
于點 ![]() ,
, ![]() ,連結
,連結 ![]() .
.
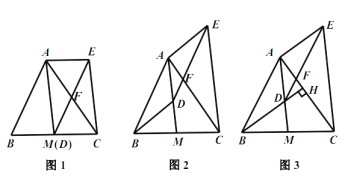
(1)如圖1,當點![]() 與
與![]() 重合時,求證:四邊形
重合時,求證:四邊形![]() 是平行四邊形
是平行四邊形
(2)如圖2,當點![]() 不與
不與![]() 重合時,(1)中的結論還成立嗎?請說明理由.
重合時,(1)中的結論還成立嗎?請說明理由.
(3)如圖3,延長![]() 交
交![]() 于點
于點![]() ,若
,若![]() ,且
,且![]() .
.
①求![]() 的度數;
的度數;
②當![]() ,
,![]() 時,求
時,求 ![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC和△ADE中,∠BAC=∠EAD,AB=AC,AD=AE,連接CD、AE交于點F.
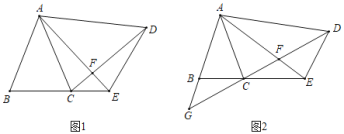
(1)求證:BE=CD.
(2)當∠BAC=∠EAD=30°,AD⊥AB時(如圖2),延長DC、AB交于點G,請直接寫出圖中除△ABC、△ADE以外的等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
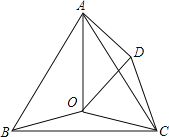
【題目】如圖,O是等邊三角形ABC內一點,∠AOB=110°,∠BOC=m°,D是△ABC外一點,且△ADC≌△BOC,連接OD.當m為_____時,△AOD是等腰三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
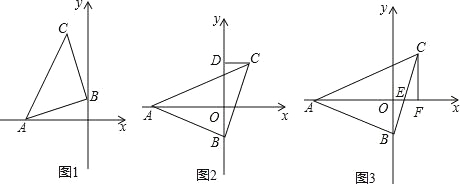
【題目】已知,△ABC 是等腰直角三角形,BC=AB,A 點在 x 負半軸上,直角頂點 B 在 y 軸上,點 C 在 x 軸上方.
(1)如圖1所示,若A的坐標是(﹣3,0),點 B的坐標是(0,1),求點 C 的坐標;
(2)如圖2,過點 C 作 CD⊥y 軸于 D,請直接寫出線段OA,OD,CD之間等量關系;
(3)如圖3,若 x 軸恰好平分∠BAC,BC與 x 軸交于點 E,過點 C作 CF⊥x 軸于 F,問 CF 與 AE 有怎樣的數量關系?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)一個不透明的盒中裝有若干個除顏色外都相同的紅球與黃球.在這個口袋中先放入2個白球,再進行摸球試驗,摸球試驗的要求:先攪拌均勻,每次摸出一個球,記錄顏色后放回盒中,再繼續摸球,全班一共做了400次這樣的摸球試驗.如果知道摸出白球的頻數是40,你能估計在未放入白球前,袋中原來共有多少個小球嗎?
(2)提出問題:一個不透明的盒中裝有若干個只有顏色不一樣的紅球與黃球,怎樣估算不同顏色球的數量?
活動操作:先從盒中摸出8個球,畫上記號放回盒中.再進行摸球試驗,摸球試驗的要求:先攪拌均勻,每次摸出一個球,記錄顏色、是否有記號,放回盒中,再繼續摸球、記錄、放回袋中.
統計結果:摸球試驗活動一共做了50次,統計結果如下表:
球的類別 | 無記號 | 有記號 | ||
紅色 | 黃色 | 紅色 | 黃色 | |
摸到的次數 | 18 | 28 | 2 | 2 |
由上述的摸球試驗推算:
①盒中紅球、黃球各占總球數的百分比分別是多少?
②盒中有紅球多少個?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com