
【題目】如圖,點![]() 在直線
在直線![]() 上,過點
上,過點![]() 作
作![]() 軸交
軸交![]() 軸于點
軸于點![]() ,以點
,以點![]() 為直角項點,
為直角項點,![]() 為直角邊在
為直角邊在![]() 的右側作等腰直角
的右側作等腰直角![]() ,再過點
,再過點![]() 作
作![]() ,分別交直線
,分別交直線![]() 和
和![]() 軸于
軸于![]() ,
,![]() 兩點,以點
兩點,以點![]() 為直角頂點,
為直角頂點,![]() 為直角邊在
為直角邊在![]() 的右側作等腰直角
的右側作等腰直角![]() ,…,按此規律進行下去,則點
,…,按此規律進行下去,則點![]() 的坐標為__________ (結果用含正整數
的坐標為__________ (結果用含正整數![]() 的代數式表示).
的代數式表示).

【答案】![]()
【解析】
先根據點A1的坐標以及A1B1∥y軸,求得B1的坐標,進而根據等腰直角三角形的性質得到B2的坐標,即可求得A2的坐標,從而求得C1的坐標,進而得到B3的坐標,求得A3的坐標,從而求得C2的坐標,最后根據根據變換規律,求得Cn的坐標.
解:∵點A1(2,1)在直線y=kx上,
∴1=2k,解得k=![]() ,
,
∴直線為y=![]() x,
x,
∵過點A1作A1B1∥y軸交x軸于點B1,以點A1為直角頂點,A1B1為直角邊在A1B1的右側作等腰直角△A1B1C1,
∴A1C1∥x軸,
∴B2(3,0),C1(3,1),
當x=3時,y=![]() x=
x=![]() ,即A2(2,
,即A2(2,![]() ),
),
∴B3(![]() ,0),
,0),
∴C2(![]() ,
,![]() ),
),
∴以此類推,
C3(![]() ,
,![]() ),
),
…
![]()
![]() ,
,
故答案為:![]()
![]()


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,直線y=x+4與拋物線y=﹣![]() x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.
x2+bx+c(b,c是常數)交于A、B兩點,點A在x軸上,點B在y軸上.設拋物線與x軸的另一個交點為點C.

(1)求該拋物線的解析式;
(2)P是拋物線上一動點(不與點A、B重合),
①如圖2,若點P在直線AB上方,連接OP交AB于點D,求![]() 的最大值;
的最大值;
②如圖3,若點P在x軸的上方,連接PC,以PC為邊作正方形CPEF,隨著點P的運動,正方形的大小、位置也隨之改變.當頂點E或F恰好落在y軸上,直接寫出對應的點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
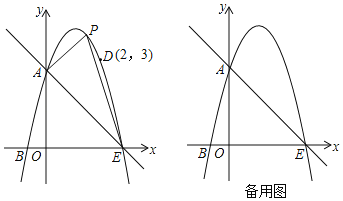
【題目】如圖,拋物線y=ax2+bx+c經過A(0,3)、B(﹣1,0)、D(2,3),拋物線與x軸的另一交點為E,點P為直線AE上方拋物線上一動點,設點P的橫坐標為t.
(1)求拋物線的表達式;
(2)當t為何值時,△PAE的面積最大?并求出最大面積;
(3)是否存在點P使△PAE為直角三角形?若存在,求出t的值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD的邊長為4,P 為BC上的動點,連接PA,作PQ⊥PA,PQ交CD于Q,連接AQ ,則AQ的最小值是( )
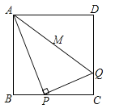
A.5B.![]() C.
C.![]() D.4
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某鄉鎮實施產業精準扶貧,幫助貧困戶承包了若干畝土地種植新品草莓,已知該草莓的成本為每千克10元,草莓成熟后投入市場銷售,經市場調查發現,草莓銷售不會虧本,且每天的銷售量y(千克)與銷售單價x(元/千克)之間函數關系如圖所示.

(1)求y與x的函數關系式,并寫出x的取值范圍.
(2)當該品種草莓的定價為多少時,每天銷售獲得利潤最大?最大利潤是多少?
(3)某村今年草莓采摘期限30天,預計產量6000千克,則按照(2)中的方式進行銷售,能否銷售完這批草莓?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我市某鄉鎮實施產業精準扶貧,幫助貧困戶承包了若干畝土地種植新品草莓,已知該草莓的成本為每千克10元,草莓成熟后投入市場銷售,經市場調查發現,草莓銷售不會虧本,且每天的銷售量y(千克)與銷售單價x(元/千克)之間函數關系如圖所示.
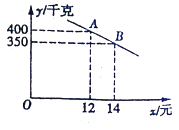
(1)求y與x的函數關系式,并寫出x的取值范圍.
(2)當該品種草莓的定價為多少時,每天銷售獲得利潤最大?最大利潤是多少?
(3)某村今年草莓采摘期限30天,預計產量6000千克,則按照(2)中的方式進行銷售,能否銷售完這批草莓?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某初中為了了解學生的視力情況,從三個年級隨機抽取了部分學生進行調查,并制作了下面的統計表和統計圖.
各年級抽查學生視力各等第人數分布統計表
優秀 | 良好 | 合格 | 不合格 | |
七年級 |
| 20 | 22 | 23 |
八年級 | 11 | 17 | 13 | 19 |
九年級 | 8 |
| 11 | 25 |
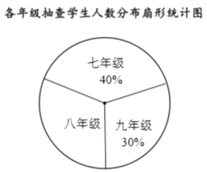
(1)在統計表中,![]() ________,
________,![]() ________;
________;
(2)在扇形統計圖中,八年級所對應的扇形圓心角為________°;
(3)若該校三個年級共有1800名學生,試估計該校學生視力等第不合格的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,拋物線y=﹣x2+bx+3與x軸和y軸的正半軸分別交于A、B兩點,且OA=OB,拋物線的頂點為M,聯結AB、AM.
(1)求這條拋物線的表達式和點M的坐標;
(2)求sin∠BAM的值;
(3)如果Q是線段OB上一點,滿足∠MAQ=45°,求點Q的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
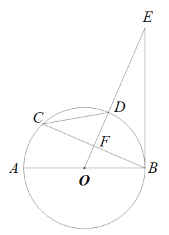
【題目】如圖,AB是⊙O的直徑, OE垂直于弦BC,垂足為F,OE交⊙O于點D,且∠CBE=2∠C.
(1)求證:BE與⊙O相切;
(2)若DF=9,tanC=![]() ,求直徑AB的長.
,求直徑AB的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com