
【題目】如圖,在△ABC中,AB=5,AC=9,S△ABC=![]() ,動點P從A點出發,沿射線AB方向以每秒5個單位的速度運動,動點Q從C點出發,以相同的速度在線段AC上由C向A運動,當Q點運動到A點時,P、Q兩點同時停止運動,以PQ為邊作正方形PQEF(P、Q、E、F按逆時針排序),以CQ為邊在AC上方作正方形QCGH.
,動點P從A點出發,沿射線AB方向以每秒5個單位的速度運動,動點Q從C點出發,以相同的速度在線段AC上由C向A運動,當Q點運動到A點時,P、Q兩點同時停止運動,以PQ為邊作正方形PQEF(P、Q、E、F按逆時針排序),以CQ為邊在AC上方作正方形QCGH.
(1)求tanA的值;
(2)設點P運動時間為t,正方形PQEF的面積為S,請探究S是否存在最小值?若存在,求出這個最小值,若不存在,請說明理由;
(3)當t為何值時,正方形PQEF的某個頂點(Q點除外)落在正方形QCGH的邊上,請直接寫出t的值.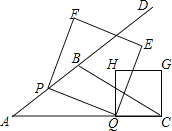
【答案】(1)![]() ;(2)S最小值=
;(2)S最小值=![]() ;(3)
;(3)![]() ;
; ![]() ;1;
;1; ![]() .
.
【解析】試題分析:(1)如圖1,過點B作BM⊥AC于點M,利用面積法求得BM的長度,利用勾股定理得到AM的長度,最后由銳角三角函數的定義進行解答;
(2)如圖2,過點P作PN⊥AC于點N.利用(1)中的結論和勾股定理得到PN2+NQ2=PQ2,所以由正方形的面積公式得到S關于t的二次函數,利用二次函數的頂點坐標公式和二次函數圖象的性質來求其最值;
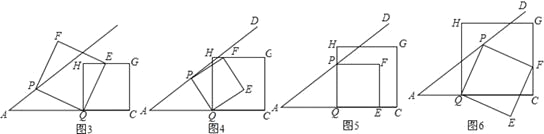
(3)需要分類討論:當點E在邊HG上、點F在邊HG上、點P邊QH(或點E在QC上)、點F邊C上時相對應的t的值.
試題解析:(1)如圖1,過點B作BM⊥AC于點M,
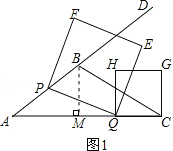
∵AC=9,S△ABC=![]() ,
,
∴![]() ACBM=
ACBM=![]() ,即
,即![]() ×9BM=
×9BM=![]() ,
,
解得BM=3.
由勾股定理,得
AM=![]() =4,
=4,
則tanA=![]() ;
;
(2)存在.如圖2,過點P作PN⊥AC于點N.依題意得AP=CQ=5t.
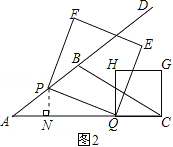
∵tanA=![]() ,
,
∴AN=4t,PN=3t.
∴QN=AC﹣AN﹣CQ=9﹣9t.
根據勾股定理得到: ![]() ,
,
S正方形PQEF= ![]() =
=![]() ﹣162t+81(0<t<
﹣162t+81(0<t<![]() ).
).
∵﹣![]() 在t的取值范圍之內,
在t的取值范圍之內,
∴S最小值=![]() ;
;
(3)①如圖3,當點E在邊HG上時,t1=![]() ;
;
②如圖4,當點F在邊HG上時,t2=![]() ;
;
③如圖5,當點P在邊QH(或點E在QC上)時,t3="1"
④如圖6,當點F在邊C上時,t4=![]() .
.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線y1=2x與雙曲線y2= ![]() 的圖象如圖所示,小明說:“滿足y1<y2的x的取值范圍是x<﹣1.”你同意他的觀點嗎? 答: . 理由是 .
的圖象如圖所示,小明說:“滿足y1<y2的x的取值范圍是x<﹣1.”你同意他的觀點嗎? 答: . 理由是 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年6月17日北京國際自行車大會召開,來自世界各地的4000多名騎游愛好者齊聚夏都延慶.各種自行車賽事也帶動了延慶的騎游產業.據調查,延慶區某騎游公司每月的租賃自行車數的增長率相同,今年四月份的騎游人數約為9000人,六月份的騎游人數約為16000人,求該騎游公司租賃自行車數的月平均增長率(精確到0.01).
查看答案和解析>>
科目:初中數學 來源: 題型:
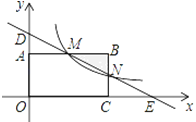
【題目】如圖,在直角坐標系中,矩形OABC的頂點O與坐標原點重合,頂點A,C分別在坐標軸上,頂點B的坐標(4,2),過點D(0,3)和E(6,0)的直線分別于AB,BC交于點M,N.
(1)求直線DE的解析式和點M的坐標;
(2)若反比例函數y=![]() (x>0)的圖象經過點M,求該反比函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
(x>0)的圖象經過點M,求該反比函數的解析式,并通過計算判斷點N是否在該函數的圖象上.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com