
【題目】如圖所示,已知∠DAB=∠DCB,AF平分∠DAB,CE平分∠DCB,∠FCE=∠CEB,試說(shuō)明:AF∥CE。

解:(1)因?yàn)?/span>∠DAB=∠DCB( ),
又AF平分∠DAB,
所以_____=![]() ∠DAB( ),
∠DAB( ),
又因?yàn)?/span>CE平分∠DCB,
所以∠FCE=_____( ),
所以∠FAE=∠FCE。
因?yàn)?/span>∠FCE=∠CEB,
所以______=________
所以AF∥CE( )
【答案】詳見(jiàn)解析.
【解析】
利用角平線的性質(zhì)和等量代換,根據(jù)已知條件,得出∠FAE=∠CEB,判斷得出AF∥CE,證得結(jié)論解決問(wèn)題.
因?yàn)椤?/span>DAB=∠DCB(已知),
又因?yàn)?/span>AF平分∠DAB,
所以∠FAE=![]() ∠DAB(角平分線的性質(zhì)).
∠DAB(角平分線的性質(zhì)).
又因?yàn)?/span>CE平分∠DCB,
所以∠FCE=![]() ∠DCB(角平分線的性質(zhì)).
∠DCB(角平分線的性質(zhì)).
所以∠FAE=∠FCE.
因?yàn)椤?/span>FCE=∠CEB,
所以∠FAE=∠CEB,
所以AF∥CE(同位角相等,兩直線平行).
故答案是:已知;∠FAE,角平分線的性質(zhì);![]() ∠DCB,角平分線的性質(zhì);∠FAE,∠CEB;同位角相等,兩直線平行.
∠DCB,角平分線的性質(zhì);∠FAE,∠CEB;同位角相等,兩直線平行.


 精英口算卡系列答案
精英口算卡系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角△ABC中,∠ACB=90°,∠B=30°,CD⊥AB于D,CE是△ABC的角平分線.
(1)求∠DCE的度數(shù).
(2)若∠CEF=135°,求證:EF∥BC.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD是正方形,以CD為邊作等邊三角形CDE,BE與AC相交于點(diǎn)M,則∠ADM的度數(shù)是_____.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,某建筑物AC頂部有一旗桿AB,且點(diǎn)A,B,C在同一條直線上,小明在地面D處觀測(cè)旗桿頂端B的仰角為30°,然后他正對(duì)建筑物的方向前進(jìn)了20米到達(dá)地面的E處,又測(cè)得旗桿頂端B的仰角為60°,已知建筑物的高度AC=12m,求旗桿AB的高度(結(jié)果精確到0.1米).參考數(shù)據(jù): ![]() ≈1.73,
≈1.73, ![]() ≈1.41.
≈1.41.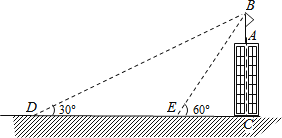
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,AB是⊙O的直徑,C是⊙O上的一點(diǎn),直線MN經(jīng)過(guò)點(diǎn)C,過(guò)點(diǎn)A作直線MN的垂線,垂足為點(diǎn)D,且∠BAC=∠CAD.
(1)求證:直線MN是⊙O的切線;
(2)若CD=3,∠CAD=30°,求⊙O的半徑.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖:四邊形ABCD中,對(duì)角線AC、BD相交于點(diǎn)O,下列條件不能判定這個(gè)四邊形是平行四邊形的是( )

A. AB//DC,AD//BC B. AB//DC,AD=BC
C. AO=CO,BO=DO D. AB=DC,AD=BC
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】隨著“互聯(lián)網(wǎng)+”時(shí)代的到來(lái),一種新型打車(chē)方式受到大眾歡迎.該打車(chē)方式的計(jì)價(jià)規(guī)則如圖①所示,若車(chē)輛以平均速度vkm/h行駛了skm,則打車(chē)費(fèi)用為(ps+60q·![]() )元(不足9元按9元計(jì)價(jià)).小明某天用該打車(chē)方式出行,按上述計(jì)價(jià)規(guī)則,其打車(chē)費(fèi)用y(元)與行駛里程x(km)的函數(shù)關(guān)系也可由如圖②表示.
)元(不足9元按9元計(jì)價(jià)).小明某天用該打車(chē)方式出行,按上述計(jì)價(jià)規(guī)則,其打車(chē)費(fèi)用y(元)與行駛里程x(km)的函數(shù)關(guān)系也可由如圖②表示.
(1)當(dāng)x≥6時(shí),求y與x的函數(shù)關(guān)系式.
(2)若p=1,q=0.5,求該車(chē)行駛的平均速度.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,DF是
,DF是![]() 的中位線,點(diǎn)C關(guān)于DF的對(duì)稱(chēng)點(diǎn)為E,以DE,EF為鄰邊構(gòu)造矩形DEFG,DG交BC于點(diǎn)H,連結(jié)CG.
的中位線,點(diǎn)C關(guān)于DF的對(duì)稱(chēng)點(diǎn)為E,以DE,EF為鄰邊構(gòu)造矩形DEFG,DG交BC于點(diǎn)H,連結(jié)CG.
![]() 求證:
求證:![]() ≌
≌![]() .
.
![]() 若
若![]() .
.
![]() 求CG的長(zhǎng).
求CG的長(zhǎng).
![]() 在
在![]() 的邊上取一點(diǎn)P,在矩形DEFG的邊上取一點(diǎn)Q,若以P,Q,C,G為頂點(diǎn)的四邊形是平行四邊形,求出所有滿(mǎn)足條件的平行四邊形的面積.
的邊上取一點(diǎn)P,在矩形DEFG的邊上取一點(diǎn)Q,若以P,Q,C,G為頂點(diǎn)的四邊形是平行四邊形,求出所有滿(mǎn)足條件的平行四邊形的面積.
![]() 在
在![]() 內(nèi)取一點(diǎn)O,使四邊形AOHD是平行四邊形,連結(jié)OA,OB,OC,直接寫(xiě)出
內(nèi)取一點(diǎn)O,使四邊形AOHD是平行四邊形,連結(jié)OA,OB,OC,直接寫(xiě)出![]() ,
,![]() ,
,![]() 的面積之比.
的面積之比.

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,CD是⊙O的直徑,弦AB⊥CD于點(diǎn)G,直線EF與⊙O相切于點(diǎn)D,則下列結(jié)論中不一定正確的是( ) 
A.AG=BG
B.AB∥EF
C.AD∥BC
D.∠ABC=∠ADC
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com