
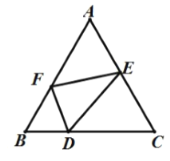
【題目】已知等邊![]() 的邊長為3,點
的邊長為3,點![]() 為
為![]() 邊上一點,且
邊上一點,且![]() ,
,![]() 分別為邊
分別為邊![]() 上的點(不包括端點),則
上的點(不包括端點),則![]() 周長的最小值為( )
周長的最小值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
作關點D關于AB的對稱點![]() ,作點D關于AC的對稱點G,連接DG與AB、AC分別交于F、E.連接
,作點D關于AC的對稱點G,連接DG與AB、AC分別交于F、E.連接![]() B、GC,延長
B、GC,延長![]() D和GC相交于點K.根據軸對稱性質可得此時三角形DEF的周長=G
D和GC相交于點K.根據軸對稱性質可得此時三角形DEF的周長=G![]() ,且最小.根據軸對稱性質和等腰三角形性質推出BH=
,且最小.根據軸對稱性質和等腰三角形性質推出BH=![]() BD=
BD=![]() ,∠CDK=∠BDH=30°,根據勾股定理求出DH,根據含有30°直角三角形性質得到D
,∠CDK=∠BDH=30°,根據勾股定理求出DH,根據含有30°直角三角形性質得到D![]() =2DH;同理,可得到∠K=90°,根據勾股定理可得DK=
=2DH;同理,可得到∠K=90°,根據勾股定理可得DK=![]() ,
,![]() .
.
作關點D關于AB的對稱點![]() ,作點D關于AC的對稱點G,連接DG與AB、AC分別交于F、E.連接
,作點D關于AC的對稱點G,連接DG與AB、AC分別交于F、E.連接![]() B、GC,延長
B、GC,延長![]() D和GC相交于點K.根據軸對稱性質可得此時三角形DEF的周長=G
D和GC相交于點K.根據軸對稱性質可得此時三角形DEF的周長=G![]() ,且最小.
,且最小.
根據軸對稱性質可得,B![]() =BD=1,∠HBD=∠HB
=BD=1,∠HBD=∠HB![]() =60°,DH⊥D
=60°,DH⊥D![]()
所以∠BDH=∠B![]() D=30°
D=30°
所以BH=![]() BD=
BD=![]() ,∠CDK=∠BDH=30°
,∠CDK=∠BDH=30°
所以在Rt△BHD中,DH=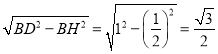
所以D![]() =2DH=
=2DH=![]()
同理,DC=CG=3-1=2,∠DCG=2∠DCE=120°
所以∠DCK=180°-∠DCG=180°-120°=60°
所以∠K=180°-30°-60°=90°
所以KC=![]()
所以GK=1+2=3,DK=![]()
所以![]()
所以![]()
故選:B


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,A(﹣3,0)、B(0,7)、C(7,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求證:∠ABO=∠CAD;
(2)求四邊形ABCD的面積;
(3)如圖2,E為∠BCO的鄰補角的平分線上的一點,且∠BEO=45°,OE交BC于點F,求BF的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一個直角三角形紙片ABO放置在平面直角坐標系中,點 ![]() ,點B(0,1),點O(0,0).P是邊AB上的一點(點P不與點A,B重合),沿著OP折疊該紙片,得點A的對應點A'.
,點B(0,1),點O(0,0).P是邊AB上的一點(點P不與點A,B重合),沿著OP折疊該紙片,得點A的對應點A'.
(1)如圖①,當點A'在第一象限,且滿足A'B⊥OB時,求點A'的坐標;
(2)如圖②,當P為AB中點時,求A'B的長;
(3)當∠BPA'=30°時,求點P的坐標(直接寫出結果即可).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點O是邊AC上一個動點,過點O作直線EF∥BC分別交∠ACB、外角∠ACD的平分線于點E、F.
(1)若CE=8,CF=6,求OC的長;
(2)連接AE、AF.問:當點O在邊AC上運動到什么位置時,四邊形AECF是矩形?并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某電器超市銷售每臺進價分別為200元、170元的A、B兩種型號的電風扇,下表是近兩周的銷售情況:
(進價、售價均保持不變,利潤 = 銷售收入-進貨成本)
(1)求A、B兩種型號的電風扇的銷售單價;

(2)若超市準備用不多于5400元的金額再采購這兩種型號的電風扇共30臺,求A種型號的電風扇最多能采購多少臺?
(3)在(2)的條件下,超市銷售完這30臺電風扇能否實現利潤為1400元的目標?若能,請給出相應的采購方案;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
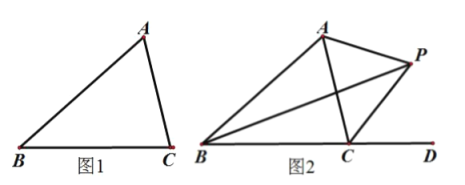
【題目】(1)如圖1,求證:三角形的三條角平分線相交于一點,并且這一點到三邊的距離相等;
(2)如圖2,若![]() 的平分線與
的平分線與![]() 外角
外角![]() 的平分線相交于點
的平分線相交于點![]() 連接
連接![]() ,若
,若![]() ,則
,則![]() 是 度.
是 度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】校學生會對七年級部分學生的課外閱讀量進行了隨機調查,整理調查結果,并根據調查結果繪制了不完整的圖表,如圖所示:
本數(本) | 頻數(人數) | 頻率 |
5 | a | 0.3 |
6 | 10 | 0.2 |
7 | 20 | b |
8 | 5 | 0.1 |
合計 | c | 1 |
(1)統計表中的b= ,c= ;請將頻數分布直方圖補充完整.
(2)所有被調查學生課外閱讀的平均本數為 本,課外閱讀書本數的中位數為 本.
(3)若該校七年級共有1200名學生,估計該校七年級學生課外閱讀6本及以下的人數為 人.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AB=6,AC=8,BC=10,P為邊BC上一動點,PE⊥AB于E,PF⊥AC于F,M為EF中點,則AM的最小值為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,請在下列四個關系中,選出兩個恰當的關系作為條件,推出四邊形ABCD是平行四邊形,并予以證明.關系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
(1)寫出所有成立的情況(只需填寫序號);
(2)選擇其中一種證明.
已知:在四邊形ABCD中, ;
求證:四邊形ABCD是平行四邊形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com