
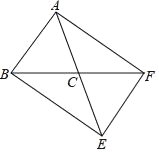
【題目】如圖,在△ABC中,AB=AC,若將△ABC繞點C順時針旋轉180°得到△EFC,連接AF、BE.
(1)求證:四邊形ABEF是平行四邊形;
(2)當∠ABC為多少度時,四邊形ABEF為矩形?請說明理由.
【答案】(1)證明見解析(2)當∠ABC=60°時,四邊形ABEF為矩形
【解析】
(1)根據旋轉得出CA=CE,CB=CF,根據平行四邊形的判定得出即可;
(2)根據等邊三角形的判定得出△ABC是等邊三角形,求出AE=BF,根據矩形的判定得出即可.
(1)∵將△ABC繞點C順時針旋轉180°得到△EFC,∴△ABC≌△EFC,∴CA=CE,CB=CF,∴四邊形ABEF是平行四邊形;
(2)當∠ABC=60°時,四邊形ABEF為矩形,理由是:∵∠ABC=60°,AB=AC,∴△ABC是等邊三角形,∴AB=AC=BC.
∵CA=CE,CB=CF,∴AE=BF.
∵四邊形ABEF是平行四邊形,∴四邊形ABEF是矩形.


科目:初中數學 來源: 題型:
【題目】列方程組解應用題:用3輛![]() 型車和2輛
型車和2輛![]() 型車載滿貨物一次可運貨17噸;用2輛
型車載滿貨物一次可運貨17噸;用2輛![]() 型車和3輛
型車和3輛![]() 型車載滿貨物一次可運貨18噸,某物流公司現有35噸貨物,計劃同時租用
型車載滿貨物一次可運貨18噸,某物流公司現有35噸貨物,計劃同時租用![]() 型車
型車![]() 輛,
輛,![]() 型車
型車![]() 輛,一次運完,且恰好每輛車都載滿貨物.
輛,一次運完,且恰好每輛車都載滿貨物.
(1)1輛![]() 型車和1輛
型車和1輛![]() 型車都載滿貨物一次可分別運貨多少噸?
型車都載滿貨物一次可分別運貨多少噸?
(2)若![]() 型車每輛需租金200元/次,
型車每輛需租金200元/次,![]() 型車每輛需租金240元/次,請你幫該物流設計最省錢的租車方案,并求出最少租車費.
型車每輛需租金240元/次,請你幫該物流設計最省錢的租車方案,并求出最少租車費.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是小亮同學設計的一個軸對稱圖形的一部分.其中點![]() 都在直角坐標系網格的格點上,每個小正方形的邊長都等于1.
都在直角坐標系網格的格點上,每個小正方形的邊長都等于1.
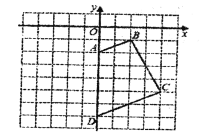
(1)請畫出關于![]() 軸成軸對稱圖形的另一半,并寫出
軸成軸對稱圖形的另一半,并寫出![]() ,
,![]() 兩點的對應點坐標.
兩點的對應點坐標.
(2)記![]() ,
,![]() 兩點的對應點分別為
兩點的對應點分別為![]() ,
,![]() ,請直接寫出封閉圖形
,請直接寫出封閉圖形![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則在下列各式子:①abc>0;②a+b+c>0;③a+c>b;④2a+b=0;⑤![]() =b2-4ac<0中,成立的式子有( )
=b2-4ac<0中,成立的式子有( )
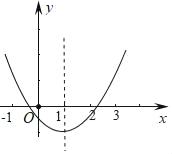
A. ②④⑤ B. ②③⑤
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠B=90°,BC=8 AB=6cm,動點P從點A開始沿邊AB向點B以1cm/s的速度移動,動點Q從點B開始沿邊BC向點C以2cm/s的速度移動.若P,Q兩點分別從A,B兩點同時出發,在運動過程中,△PBQ的最大面積是( )
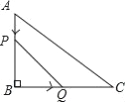
A. 18cm2 B. 12cm2 C. 9cm2 D. 3cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算下列各題.
①(x2+3)(3x2﹣1)
②(4x2y﹣8x3y3)÷(﹣2x2y)
③[(m+3)(m﹣3)]2
④10﹣2×100+105÷103
⑤![]()
⑥![]() ,其中x滿足x2﹣x﹣1=0.
,其中x滿足x2﹣x﹣1=0.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com