
【題目】如圖所示,![]() 的頂點A在反比例函數
的頂點A在反比例函數![]() 的圖像上,直線AB交y軸于點C,且點C的縱坐標為5,過點A、B分別作y軸的垂線AE、BF,垂足分別為點E、F,且
的圖像上,直線AB交y軸于點C,且點C的縱坐標為5,過點A、B分別作y軸的垂線AE、BF,垂足分別為點E、F,且![]() .
.

(1)若點E為線段OC的中點,求k的值;
(2)若![]() 為等腰直角三角形,
為等腰直角三角形,![]() ,其面積小于3.
,其面積小于3.
①求證:![]() ;
;
②把![]() 稱為
稱為![]() ,
,![]() 兩點間的“ZJ距離”,記為
兩點間的“ZJ距離”,記為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)①見解析;②8.
;(2)①見解析;②8.
【解析】
(1)由點E為線段OC的中點,可得E點坐標為![]() ,進而可知A點坐標為:
,進而可知A點坐標為:![]() ,代入解析式即可求出k;
,代入解析式即可求出k;
(2)①由![]() 為等腰直角三角形,可得
為等腰直角三角形,可得![]() ,再根據同角的余角相等可證
,再根據同角的余角相等可證![]() ,由AAS即可證明
,由AAS即可證明![]() ;
;
②由“ZJ距離”的定義可知![]() 為MN兩點的水平距離與垂直距離之和,故
為MN兩點的水平距離與垂直距離之和,故![]() ,即只需求出B點坐標即可,設點
,即只需求出B點坐標即可,設點![]() ,由
,由![]() 可得
可得![]() ,進而代入直線AB解析式求出k值即可解答.
,進而代入直線AB解析式求出k值即可解答.
解:(1)∵點E為線段OC的中點,OC=5,
∴![]() ,即:E點坐標為
,即:E點坐標為![]() ,
,
又∵AE⊥y軸,AE=1,
∴![]() ,
,
∴![]() .
.
(2)①在![]() 為等腰直角三角形中,
為等腰直角三角形中,![]() ,
,![]() ,
,
∴![]() ,
,
又∵BF⊥y軸,
∴![]() ,
,
∴![]()
在![]() 和
和![]() 中
中
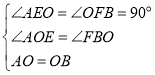 ,
,
∴![]() ,
,
②解:設點![]() 坐標為
坐標為![]() ,
,
∵![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
設直線AB解析式為:![]() ,將AB兩點代入得:
,將AB兩點代入得:
則![]() .
.
解得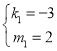 ,
,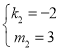 .
.
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,符合;
,符合;
∴![]()
![]()
![]()
![]()
![]()
![]() ,
,
當![]() 時,
時,![]() ,
,![]() ,
,![]() ,不符,舍去;
,不符,舍去;
綜上所述:![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】定義:對于已知的兩個函數,任取自變量![]() 的一個值,當
的一個值,當![]() 時,它們對應的函數值相等;當
時,它們對應的函數值相等;當![]() 時,它們對應的函數值互為相反數,我們稱這樣的兩個函數互為相關函數.例如:正比例函數
時,它們對應的函數值互為相反數,我們稱這樣的兩個函數互為相關函數.例如:正比例函數![]() ,它的相關函數為
,它的相關函數為![]() .
.
(1)已知點![]() 在一次函數
在一次函數![]() 的相關函數的圖像上,求
的相關函數的圖像上,求![]() 的值;
的值;
(2)已知二次函數![]() .
.
①當點![]() 在這個函數的相關函數的圖像上時,求
在這個函數的相關函數的圖像上時,求![]() 的值;
的值;
②當![]() 時,求函數
時,求函數![]() 的相關函數的最大值和最小值.
的相關函數的最大值和最小值.
(3)在平面直角坐標系中,點![]() 、
、![]() 的坐標分別為
的坐標分別為![]() 、
、![]() ,連結
,連結![]() .直接寫出線段
.直接寫出線段![]() 與二次函數
與二次函數![]() 的相關函數的圖像有兩個公共點時
的相關函數的圖像有兩個公共點時![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
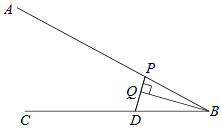
【題目】如圖,點D是射線BC上的一定點,點P是線段AB上一動點,連接PD,作BQ垂直PD,交直線PD于點Q.小騰根據學習函數的經驗,對線段PB,PD,BQ的長度之間的關系進行了探究.下面是小騰的探究過程,請補充完整:
(1)對于點P在AB上的不同位置,畫圖、測量,得到了線段PB,PD,BQ的長度的幾組值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | |
BP/cm | 0.00 | 1.00 | 2.00 | 3.00 | 4.00 | 5.00 | 6.00 |
PD/cm | 2.00 | 1.22 | 0.98 | 1.56 | 2.43 | 3.38 | 4.35 |
BQ/cm | 0.00 | 0.78 | 1.94 | 1.82 | 1.56 | 1.41 | 1.31 |
在PB,PD,BQ的長度這三個量中,確定 的長度是自變量, 的長度和 的長度都是這個自變量的函數;
(2)在同一平面直角坐標系xOy中,畫出(1)中所確定的函數的圖象;
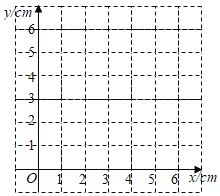
(3)結合函數圖象,解決問題:當PD>BQ時,PB長度范圍是 cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
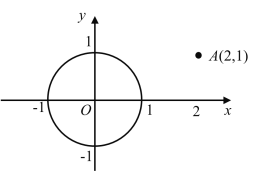
【題目】我們知道,兩點之間線段最短,因此,連接兩點間線段的長度叫做兩點間的距離;同理,連接直線外一點與直線上各點的所有線段中,垂線段最短,因此,直線外一點到這條直線的垂線段的長度,叫做點到直線的距離.類似地,連接曲線外一點與曲線上各點的所有線段中,最短線段的長度,叫做點到曲線的距離.依此定義,如圖,在平面直角坐標系中,點![]() 到以原點為圓心,以1為半徑的圓的距離為_____.
到以原點為圓心,以1為半徑的圓的距離為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
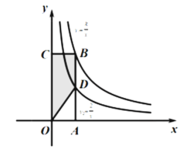
【題目】如圖所示,在平面直角坐標系Oxy中,四邊形OABC為矩形,點A、C分別在x軸、y軸上,點B在函數![]() (
(![]() ,k為常數且
,k為常數且![]() )的圖象上,邊AB與函數
)的圖象上,邊AB與函數![]() 的圖象交于點D,則陰影部分ODBC的面積為________(結果用含k的式子表示)
的圖象交于點D,則陰影部分ODBC的面積為________(結果用含k的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣![]() x2﹣
x2﹣![]() x+
x+![]() 與x軸交于點A,B(點A在點B的左邊),與y軸交于點C,點D是該拋物線的頂點.
與x軸交于點A,B(點A在點B的左邊),與y軸交于點C,點D是該拋物線的頂點.
(1)如圖1,連接CD,求線段CD的長;
(2)如圖2,點P是直線AC上方拋物線上一點,PF⊥x軸于點F,PF與線段AC交于點E;將線段OB沿x軸左右平移,線段OB的對應線段是O1B1,當PE+![]() EC的值最大時,求四邊形PO1B1C周長的最小值,并求出對應的點O1的坐標;
EC的值最大時,求四邊形PO1B1C周長的最小值,并求出對應的點O1的坐標;
(3)如圖3,點H是線段AB的中點,連接CH,將△OBC沿直線CH翻折至△O2B2C的位置,再將△O2B2C繞點B2旋轉一周在旋轉過程中,點O2,C的對應點分別是點O3,C1,直線O3C1分別與直線AC,x軸交于點M,N.那么,在△O2B2C的整個旋轉過程中,是否存在恰當的位置,使△AMN是以MN為腰的等腰三角形?若存在,請直接寫出所有符合條件的線段O2M的長;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖一,菱形![]() 與菱形
與菱形![]() 的頂點
的頂點![]() 重合,點
重合,點![]() 在對角線
在對角線![]() 上,且
上,且![]() .
.
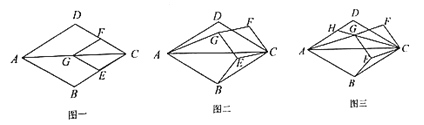
(1)問題發現:
![]() 的值為________;
的值為________;
(2)探究與證明:
將菱形![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 角(
角(![]() ),如圖二所示,試探究線段
),如圖二所示,試探究線段![]() 與
與![]() 之間的數量關系,并說明理由;
之間的數量關系,并說明理由;
(3)拓展與運用:
菱形![]() 在旋轉過程中,當點
在旋轉過程中,當點![]() ,
,![]() ,
,![]() 三點在一條直線上時,如圖三所示,連接
三點在一條直線上時,如圖三所示,連接![]() 并延長,交
并延長,交![]() 于點
于點![]() ,若
,若![]() ,
,![]() ,則
,則![]() 的長為________.
的長為________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為獎勵優秀學生,某校準備購買一批文具袋和圓規作為獎品,已知購買1個文具袋和2個圓規需21元,購買2個文具袋和3個圓規需39元.
(1)求文具袋和圓規的單價.
(2)學校準備購買文具袋20個,圓規100個,文具店給出兩種優惠方案:
方案一:每購買一個文具袋贈送1個圓規.
方案二:購買10個以上圓規時,超出10個的部分按原價的八折優惠,文具袋不打折.學校選擇哪種方案更劃算?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數![]() 的圖象與反比例函數
的圖象與反比例函數![]() 的圖象交于
的圖象交于![]() .
.
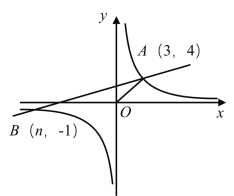
(1)求反比例函數和一次函數的解析式;
(2)在x軸上存在一點C,使![]() 為等腰三角形,求此時點C的坐標;
為等腰三角形,求此時點C的坐標;
(3)根據圖象直接寫出使一次函數的值大于反比例函數的值的x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com