
【題目】已知![]() 中,
中,![]() ,
,![]() ,點
,點![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上(不與端點重合),
上(不與端點重合),![]() ,射線
,射線![]() 交
交![]() 延長線于點
延長線于點![]() ,點
,點![]() 在直線
在直線![]() 上,
上,![]() .
.
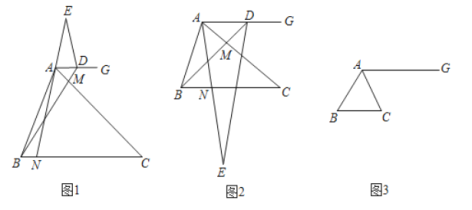
(1)(觀察猜想)如圖1,點![]() 在射線
在射線![]() 上,當(dāng)
上,當(dāng)![]() 時,
時,
①線段![]() 與
與![]() 的數(shù)量關(guān)系是______;
的數(shù)量關(guān)系是______;
②![]() 的度數(shù)是______;
的度數(shù)是______;
(2)(探究證明)如圖2點![]() 在射線
在射線![]() 上,當(dāng)
上,當(dāng)![]() 時,判斷并證明線段
時,判斷并證明線段![]() 與
與![]() 的數(shù)量關(guān)系,求
的數(shù)量關(guān)系,求![]() 的度數(shù);
的度數(shù);
(3)(拓展延伸)如圖3,點![]() 在直線
在直線![]() 上,當(dāng)
上,當(dāng)![]() 時,
時,![]() ,點
,點![]() 是
是![]() 邊上的三等分點,直線
邊上的三等分點,直線![]() 與直線
與直線![]() 交于點
交于點![]() ,請直接寫出線段
,請直接寫出線段![]() 的長.
的長.
【答案】(1)①![]() ,②
,②![]() ;(2)
;(2)![]() ;(3)滿足條件的
;(3)滿足條件的![]() 的長為
的長為![]() 或4.
或4.
【解析】
(1)①延長![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點O,先由等邊對等角得到
于點O,先由等邊對等角得到![]() ,然后證明
,然后證明![]() ,即可得到BM=AN;②再由等邊對等角和平行線推出
,即可得到BM=AN;②再由等邊對等角和平行線推出![]() ,由三角形外角性質(zhì)得到
,由三角形外角性質(zhì)得到![]() ,可推出
,可推出![]() ,即可得
,即可得![]() .
.
(2)同理可證![]() ,同(1)可推出
,同(1)可推出 ![]() ,最后得到
,最后得到![]() .
.
(3)當(dāng)![]() 時,作
時,作![]() 于
于![]() ,在
,在![]() 中,利用60°可求出邊長,然后在在
中,利用60°可求出邊長,然后在在![]() 中求出BM,再由
中求出BM,再由![]() ,利用相似比求出CF,當(dāng)
,利用相似比求出CF,當(dāng)![]() 時,同法可求
時,同法可求![]() .
.
(1)①如圖1中,延長![]() 交
交![]() 于點
于點![]() ,交
,交![]() 于點O.
于點O.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ;
;
②∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∵∠ANB+∠ENF=180°,∠BMA+∠BMC=180°,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
故答案為①![]() ,②
,②![]() .
.
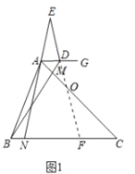
(2)如圖2中,設(shè)![]() 交
交![]() 于點
于點![]() .
.
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

(3)①如圖3-1中,當(dāng)![]() 時,作
時,作![]() 于
于![]() .
.
由題意![]() ,在
,在![]() 中,
中,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
在![]() 中,
中,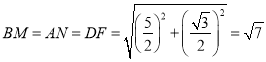 ,
,
由(2)可知:![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
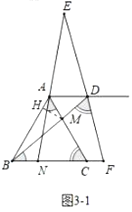
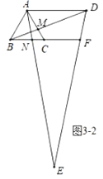
②如圖3-2中,當(dāng)![]() 時,同法可得
時,同法可得![]() .
.
綜上所述,滿足條件的![]() 的長為
的長為![]() 或4.
或4.


科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC三個頂點的坐標(biāo)分別為A(1,1),B(4,2),C(3,4)
(1)請畫出將△ABC向左平移4個單位長度后得到的圖形△A1B1C1;
(2)請畫出△ABC關(guān)于原點O成中心對稱的圖形△A2B2C2;
(3)在x軸上找一點P,使PA+PB的值最小,請直接寫出點P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
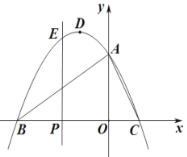
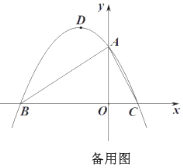
【題目】如圖,在平面直角坐標(biāo)系中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 與
與![]() 軸交于
軸交于![]() 、
、![]() 兩點
兩點
(點![]() 在點
在點![]() 的左側(cè)),拋物線的頂點為
的左側(cè)),拋物線的頂點為![]() .
.
(1)求拋物線的表達(dá)式;
(2)用配方法求點![]() 的坐標(biāo);
的坐標(biāo);
(3)點![]() 是線段
是線段![]() 上的動點.
上的動點.
①過點![]() 作
作![]() 軸的垂線交拋物線于點
軸的垂線交拋物線于點![]() ,若
,若![]() ,求點
,求點![]() 的坐標(biāo);
的坐標(biāo);
②在①的條件下,點![]() 是坐標(biāo)軸上的點,且點
是坐標(biāo)軸上的點,且點![]() 到
到![]() 和
和![]() 的距離相等,請直接寫出線段
的距離相等,請直接寫出線段![]() 的長;
的長;
③若點![]() 是射線
是射線![]() 上的動點,且始終滿足
上的動點,且始終滿足![]() ,連接
,連接![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在□ABCD中,E為BC的中點,過點E作EF⊥AB于點F,延長DC,交FE的延長線于點G,連結(jié)DF,已知∠FDG=45°
(1)求證:GD=GF.
(2)已知BC=10, ![]() .求 CD的長.
.求 CD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
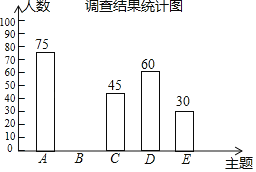
【題目】2019年3月19日,河南省教育廳發(fā)布《關(guān)于推進中小學(xué)生研學(xué)旅行的實施方案》,某中學(xué)為落實方案,給學(xué)生提供了以下五種主題式研學(xué)線路:A.“紅色河南”,B.“厚重河南”C.“出彩河南”,D.“生態(tài)河南”,E.“老家河南”為了解學(xué)生最喜歡哪一種研學(xué)線路(每人只選取一種),隨機抽取了部分學(xué)生進行調(diào)查,將調(diào)查結(jié)果繪制成如下不完整的統(tǒng)計表和統(tǒng)計圖.根據(jù)以上信息解答下列問題:
調(diào)查結(jié)果統(tǒng)計表
主題 | 人數(shù)/人 | 百分比 |
A | 75 | n% |
B | m | 30% |
C | 45 | 15% |
D | 60 | |
E | 30 |
(1)本次接受調(diào)查的總?cè)藬?shù)為 人,統(tǒng)計表中m= ,n= .
(2)補全條形統(tǒng)計圖.
(3)若把條形統(tǒng)計圖改為扇形統(tǒng)計圖,則“生態(tài)河南”主題線路所在扇形的圓心角度是 .
(4)若該實驗中學(xué)共有學(xué)生3000人,請據(jù)此估計該校最喜歡“老家河南”主題線路的學(xué)生有多少人.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,拋物線![]() 的圖象經(jīng)過
的圖象經(jīng)過![]() 和
和![]() 兩點,且與
兩點,且與![]() 軸交于
軸交于![]() ,直線
,直線![]() 是拋物線的對稱軸,過點
是拋物線的對稱軸,過點![]() 的直線
的直線![]() 與直線相交于點
與直線相交于點![]() ,且點
,且點![]() 在第一象限.
在第一象限.

(1)求該拋物線的解析式;
(2)若直線![]() 和直線
和直線![]() 、
、![]() 軸圍成的三角形面積為6,求此直線的解析式;
軸圍成的三角形面積為6,求此直線的解析式;
(3)點![]() 在拋物線的對稱軸上,
在拋物線的對稱軸上,![]() 與直線
與直線![]() 和
和![]() 軸都相切,求點
軸都相切,求點![]() 的坐標(biāo).
的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,依次連接第一個矩形各邊的中點得到一個菱形,再依次連接菱形各邊的中點得到第二個矩形,按照此方法繼續(xù)下去.已知第一個矩形的兩條鄰邊長分別為6和8,則第n個菱形的周長為______.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某無人機興趣小組在操場上開展活動(如圖),此時無人機在離地面30米的D處,無人機測得操控者A的俯角為37°,測得點C處的俯角為45°.又經(jīng)過人工測量操控者A和教學(xué)樓BC距離為57米,求教學(xué)樓BC的高度.(注:點A,B,C,D都在同一平面上.參考數(shù)據(jù):sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
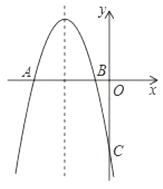
【題目】如圖所示,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點,
兩點,![]() ,與
,與![]() 軸交于
軸交于![]() ,并且對稱軸
,并且對稱軸![]() .
.

(1)求拋物線的解析式;
(2)![]() 在
在![]() 軸上方的拋物線上,過
軸上方的拋物線上,過![]() 的直線
的直線![]() 與直線
與直線![]() 交于點
交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() ,求
,求![]() 的最大值;
的最大值;
(3)點![]() 為拋物線對稱軸上一點,當(dāng)
為拋物線對稱軸上一點,當(dāng)![]() 是以
是以![]() 為直角邊的直角三角形時,求
為直角邊的直角三角形時,求![]() 點坐標(biāo);
點坐標(biāo);
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com