
【題目】閱讀材料:以下是我們教科書中的一段內容,請仔細閱讀,并解答有關問題.
公元前3世紀,古希臘學家阿基米德發現:若杠桿上的兩物體與支點的距離與其重量成反比,則杠桿平衡,后來人們把它歸納為“杠桿原理”,通俗地說,杠桿原理為:
阻力×阻力臂=動力×動力臂

(問題解決)
若工人師傅欲用撬棍動一塊大石頭,已知阻力和阻力臂不變,分別為1500N和0.4m.
(1)動力F(N)與動力臂l(m)有怎樣的函數關系?當動力臂為1.5m時,撬動石頭需要多大的力?
(2)若想使動力F(N)不超過題(1)中所用力的一半,則動力臂至少要加長多少?
(數學思考)
(3)請用數學知識解釋:我們使用棍,當阻力與阻力臂一定時,為什么動力臂越長越省力.

【答案】400N;1.5米;見解析
【解析】
試題(1)、根據杠桿定律求得函數的解析式后代入l=1.5求得力的大小即可;(2)、將求得的函數解析式變形后求得動力臂的大小,然后即可求得增加的長度;(3)、利用反比例函數的知識結合杠桿定律進行說明即可.
試題解析:(1)、根據“杠桿定律”有FL=1500×0.4, ∴函數的解析式為F=![]() ,
,
當L=1.5時,F=![]() =400, 因此,撬動石頭需要400N的力;
=400, 因此,撬動石頭需要400N的力;
(2)、由(1)知FL=600, ∴函數解析式可以表示為:L=![]() , 當F=400×
, 當F=400×![]() =200時,L=3,
=200時,L=3,
3﹣1.5=1.5(m), 因此若用力不超過400N的一半,則動力臂至少要加長1.5米;
(3)、因為撬棍工作原理遵循“杠桿定律”,當阻力與阻力臂一定時,其乘積為常數,設其為k,則動力F與動力臂L的函數關系式為F=![]() ,根據反比例函數的性質可知,動力F隨動力臂l的增大而減小,所以動力臂越長越省力.
,根據反比例函數的性質可知,動力F隨動力臂l的增大而減小,所以動力臂越長越省力.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
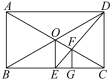
【題目】如圖,在矩形ABCD中,對角線AC、BD相交于點O,過點O作OE⊥BC于E點,連接DE交OC于F點,作FG⊥BC于G點,則△ABC與△FGC是位似圖形嗎?若是,請說出位似中心,并求出相似比;若不是,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知⊙O的半徑為10,圓心O到弦AB的距離為5,則弦AB所對的圓周角的度數是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中數學 來源: 題型:
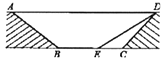
【題目】為緩解交通擁堵,某區擬計劃修建一地下通道,該通道一部分的截面如圖所示(圖中地面![]() 與通道
與通道![]() 平行),通道水平寬度
平行),通道水平寬度![]() 為8米,
為8米, ![]() ,通道斜面
,通道斜面![]() 的長為6米,通道斜面
的長為6米,通道斜面![]() 的坡度
的坡度![]() .
.
(1)求通道斜面![]() 的長為 米;
的長為 米;
(2)為增加市民行走的舒適度,擬將設計圖中的通道斜面![]() 的坡度變緩,修改后的通道斜面
的坡度變緩,修改后的通道斜面![]() 的坡角為30°,求此時
的坡角為30°,求此時![]() 的長.(結果保留根號)
的長.(結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一塊直角三角板的直角頂點P放在矩形ABCD的BC邊上,并且使一條直角邊經過點D,另一條直角邊與AB交于點Q.
(1)請你寫出一對相似三角形,并加以證明;
(2)若AB=6,BC=8,當PD=3PQ時,求PC的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商貿公司購進某種水果的成本為20元/千克,經過市場調研發現,這種水果在未來48天的售價p(元/千克)與時間t(天)之間的函數表達式為
p=
且其日銷售量y(kg)與時間t(天)的關系如下表:
時間t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日銷售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y與t之間的變化規律符合一次函數關系,試求第30天的日銷售量是多少?
(2)問:哪一天的銷售利潤最大?最大日銷售利潤為多少?
(3)在實際銷售的前24天中,公司決定每銷售1 kg水果就捐贈n元利潤(n<9)給“精準扶貧”對象.現發現:在前24天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫州某企業安排65名工人生產甲、乙兩種產品,每人每天生產2件甲或1件乙,甲產品每件可獲利15元.根據市場需求和生產經驗,乙產品每天產量不少于5件,當每天生產5件時,每件可獲利120元,每增加1件,當天平均每件獲利減少2元.設每天安排x人生產乙產品.
(1)根據信息填表
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生產甲產品可獲得的利潤比生產乙產品可獲得的利潤多550元,求每件乙產品可獲得的利潤.
(3)該企業在不增加工人的情況下,增加生產丙產品,要求每天甲、丙兩種產品的產量相等.已知每人每天可生產1件丙(每人每天只能生產一件產品),丙產品每件可獲利30元,求每天生產三種產品可獲得的總利潤W(元)的最大值及相應的x值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線y=-x+3與y軸交于點A,與反比例函數y=![]() (k≠0)的圖象交于點C,過點C作CB⊥x軸于點B,AO=3BO,則反比例函數的解析式為( )
(k≠0)的圖象交于點C,過點C作CB⊥x軸于點B,AO=3BO,則反比例函數的解析式為( )

A. y=![]() B. y=-
B. y=-![]() C. y=
C. y=![]() D. y=-
D. y=-![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com