
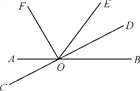
【題目】如圖,直線AB與CD相交于點O,OF,OD分別是∠AOE,∠BOE的平分線.
(1)寫出∠DOE的補角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度數;
(3)試問射線OD與OF之間有什么特殊的位置關系?為什么?
【答案】(1) ∠COE,∠AOD,∠BOC;(2)∠AOD=149°,∠EOF=59°;(3) 射線OD與OF互相垂直,理由見解析.
【解析】試題分析:(1)根據互補的定義確定∠DOE的補角;
(2)先根據角平分線的定義得出∠BOD的度數,再由鄰補角定義可得∠AOD=180°-∠BOD;之后根據鄰補角定義可得∠AOE=180°-∠BOE,再由角平分線的定義得出∠EOF的度數;
(3)運用平角的定義和角平分線的定義,證明∠DOF是90°,得直線OD、OF的位置關系.
解:(1)∠DOE的補角為:∠COE,∠AOD,∠BOC.
(2)∵OD是∠BOE的平分線,∠BOE=62°,
∴∠BOD=![]() ∠BOE=31°.
∠BOE=31°.
∴∠AOD=180°-∠BOD=149°.
∴∠AOE=180°-∠BOE=118°.
又∵OF是∠AOE的平分線,
∴∠EOF=![]() ∠AOE=59°.
∠AOE=59°.
(3)射線OD與OF互相垂直.理由如下:
∵OF,OD分別是∠AOE,∠BOE的平分線,
∴∠DOF=∠DOE+∠EOF=![]() ∠BOE+
∠BOE+![]() ∠EOA=
∠EOA=![]() (∠BOE+∠EOA)=
(∠BOE+∠EOA)=![]() ×180°=90°.
×180°=90°.
∴OD⊥OF.


 導學教程高中新課標系列答案
導學教程高中新課標系列答案科目:初中數學 來源: 題型:
【題目】某校為開展好大課間活動,欲購買單價為20元的排球和單價為80元的籃球共100個.
(1)設購買排球數為x(個),購買兩種球的總費用為y(元),請你寫出y與x的函數關系式(不要求寫出自變量的取值范圍);
(2)如果購買兩種球的總費用不超過6620元,并且籃球數不少于排球數的3倍,那么有哪幾種購買方案?
(3)從節約開支的角度來看,你認為采用哪種方案更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
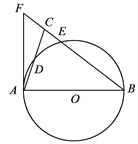
【題目】如圖,在△ABC中,BA=BC,以AB為直徑的⊙O分別交AC,BC于點D,E,BC的延長線與⊙O的切線AF交于點F.
(1)求證:∠ABC=2∠CAF;
(2)若AC=![]() ,
, ![]() ,求BE的長.
,求BE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形OABC中,AO=10,AB=8,沿直線CD折疊矩形OABC的一邊BC,使點B落在OA邊上的點E處,分別以OC,OA所在的直線為x軸,y軸建立平面直角坐標系,拋物線y=ax2+bx+c經過O,D,C三點.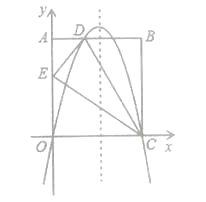
(1)求AD的長及拋物線的解析式;
(2)一動點P從點E出發,沿EC以每秒2個單位長的速度向點C運動,同時動點Q從點C出發,沿CO以每秒1個單位長的速度向點O運動,當點P運動到點C時,兩點同時停止運動,設運動時間為t秒,當t為何值時,以P,Q,C為頂點的三角形與ADE相似?
(3)點N在拋物線對稱軸上,點M在拋物線上,是否存在這樣的點M與點N,使以M,N,C,E為頂點的四邊形是平行四邊形?若存在,請直接寫出點M與點N的坐標(不寫求解過程);若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(8分). 目前節能燈在各城市已基本普及,今年某市面向縣級及農村地區推廣,為響應號召,朝陽燈飾商場用了4200元購進甲型和乙型兩種節能燈.這兩種型號節能燈的進價、售價如表:
進價(元/只) | 售價(元/只) | |
甲型 | 25 | 30 |
乙型 | 45 | 60 |
特別說明:毛利潤=售價﹣進價
(1)朝陽燈飾商場銷售甲型節能燈一只毛利潤是 元;
(2)朝陽燈飾商場購買甲,乙兩種節能燈共100只,其中買了甲型節能燈多少只?
(3)現在朝陽燈飾商場購進甲型節能燈m只,銷售完節能燈時所獲的毛利潤為1080元.求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校九年級學生共900人,為了解這個年級學生的體能,從中隨機抽取部分學生進行1 min的跳繩測試,并指定甲、乙、丙、丁四名同學對這次測試結果的數據作出整理,下圖是這四名同學提供的部分信息:
甲:將全體測試數據分成6組繪成直方圖(如圖);
乙:跳繩次數不少于105次的同學占96%;
丙:第①、②兩組頻率之和為0.12,且第②組與第⑥組頻數都是12;
丁:第②、③、④組的頻數之比為4:17:15。

根據這四名同學提供的材料,下面有四個推斷:
①這次跳繩測試共抽取了150人;②該年級跳繩次數的中位數在115~125之間
③第4組的人數為45人 ④如果跳繩次數不少于135次為優秀,根據這次調查結果,估計全年級達到跳繩優秀的人數可以超過250人,其中合理的個數是( )
A. 1個 B. 2個 C. 3個 D. 4個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com