
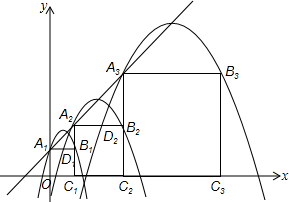
 在平面直角坐標系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如圖的方式放置.點A1,A2,A3,…,An和點C1,C2,C3,…,Cn分別落在直線y=x+1和x軸上.拋物線L1過點A1,B1,且頂點在直線y=x+1上,拋物線L2過點A2,B2,且頂點在直線y=x+1上,…,按此規律,拋物線Ln過點An,Bn,且頂點也在直線y=x+1上,其中拋物線L2交正方形A1B1C1O的邊A1B1于點D1,拋物線L3交正方形A2B2C2C1的邊A2B2于點D2,…,拋物線Ln+1交正方形AnBnCnCn-1的邊AnBn于點Dn(其中n≥2且n為正整數).
在平面直角坐標系xOy中,正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如圖的方式放置.點A1,A2,A3,…,An和點C1,C2,C3,…,Cn分別落在直線y=x+1和x軸上.拋物線L1過點A1,B1,且頂點在直線y=x+1上,拋物線L2過點A2,B2,且頂點在直線y=x+1上,…,按此規律,拋物線Ln過點An,Bn,且頂點也在直線y=x+1上,其中拋物線L2交正方形A1B1C1O的邊A1B1于點D1,拋物線L3交正方形A2B2C2C1的邊A2B2于點D2,…,拋物線Ln+1交正方形AnBnCnCn-1的邊AnBn于點Dn(其中n≥2且n為正整數).分析 (1)由直線解析式可求得A1的坐標,由正方形的性質則可求得B1坐標,由題意可求得A2的橫坐標,則可求得其縱坐標,再利用正方形的性質可求得B2的坐標,同理可求得B3的坐標;
(2)由對稱性可求得拋物線的對稱軸,則可求得其頂點坐標,再結合已知點的坐標可求得拋物線解析式,可寫出L2、L3的解析式;利用An、Bn的變化規律,可求得拋物線Ln的頂點坐標;
(3)由拋物線L2的解析式可求得A1D1的長,則可求得k1,同理可求得k2,從而可求得兩者之間的數量關系.
解答 解:
(1)∵A1在直線y=x+1上,
∴A1的坐標為(0,1),
∴A1B1=OA1=1,
∴B1(1,1),
∴A2橫坐標為1,且在直線y=x+1上,
∴A2(1,2),
∴A2B2=A2C1=2,
∴B2(3,2),同理B3(7,4),
故答案為:(1,1);(3,2);(7,4);
(2)拋物線L2、L3的解析式分別為y=-(x-2)2+3,y=-$\frac{1}{2}$(x-5)2+6;
拋物線L2的解析式的求解過程如下:
對于直線y=x+1,設x=0,可得y=1,
∴A1(0,1),
∵四邊形A1B1C1O是正方形,
∴C1(1,0),又點A2在直線y=x+1上,
∴可得點A2(1,2),
又∵B2的坐標為(3,2),
∴拋物線L2的對稱軸為直線x=2,
∴拋物線L2的頂點為(2,3),
設拋物線L2的解析式為:y=a(x-2)2+3,
∵L2過點B2(3,2),
∴2=a×(3-2)2+3,解得a=-1,
∴拋物線L2的解析式為y=-(x-2)2+3;
猜想拋物線Ln的頂點坐標為(3×2n-2-1,3×2n-2).
證明如下:
由正方形AnBnCnCn-1頂點An,Bn的坐標規律為An(2n-1-1,2n-1)與Bn(2n-1,2n-1),
∴拋物線Ln的對稱軸為直線x=$\frac{{2}^{n-1}-1+{2}^{n}-1}{2}$=3×2n-2-1,又頂點在直線y=x+1上,
∴y=3×2n-2,
∴拋物線Ln的頂點坐標為(3×2n-2-1,3×2n-2);
(3)k1與k2的數量關系為k1=k2.
理由如下:
由(2)得L2的解析式為y=-(x-2)2+3,
當y=1時,1=-(x-2)2+3,解得x1=2-$\sqrt{2}$,x2=2+$\sqrt{2}$,
∵0<A1D1<1,
∴x=2-$\sqrt{2}$,
∴A1D1=2-$\sqrt{2}$=$\sqrt{2}$($\sqrt{2}$-1),
∴D1B1=1-(2-$\sqrt{2}$)=$\sqrt{2}$-1,
∴A1D1=$\sqrt{2}$•D1B1,即k1=$\sqrt{2}$;
同理可求得A2D2=4-2 $\sqrt{2}$=2 $\sqrt{2}$($\sqrt{2}$-1),
D2B2=2-(4-2 $\sqrt{2}$)=2 $\sqrt{2}$-2=2($\sqrt{2}$-1),
∴A2D2=$\sqrt{2}$•D2B2,即k2=$\sqrt{2}$,
∴k1=k2.
點評 本題為二次函數的綜合應用,涉及正方形的性質、函數圖象上點的坐標特征、待定系數法、函數圖象的交點等知識.在(1)中求得An的橫坐標是解題的關鍵,注意正方形性質的應用,在(2)中利用待定系數法可求得拋物線解析式,求拋物線頂點坐標時注意其變化規律,在(3)中利用函數圖象的交點求得相應線段的長分別求得k1和k2的值是解題的關鍵.本題考查知識點較多,綜合性較強,難度較大.


 英才計劃同步課時高效訓練系列答案
英才計劃同步課時高效訓練系列答案科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{x-1}$ | B. | $\frac{1}{1-x}$ | C. | $\frac{1-2x}{x-1}$ | D. | $\frac{2x-1}{x-1}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
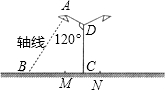 要在寬為36m的公路的綠化帶MN(寬為4m)的中央安裝路燈,路燈的燈臂AD的長為3m,且與燈柱CD成120°(如圖所示),路燈采用圓錐形燈罩,燈罩的軸線AB與燈臂垂直.當燈罩的軸線通過公路路面一側的中間時(除去綠化帶的路面部分),照明效果最理想,問:應設計多高的燈柱,才能取得最理想的照明效果?(精確到0.01m,參考數據$\sqrt{3}$≈1.732)
要在寬為36m的公路的綠化帶MN(寬為4m)的中央安裝路燈,路燈的燈臂AD的長為3m,且與燈柱CD成120°(如圖所示),路燈采用圓錐形燈罩,燈罩的軸線AB與燈臂垂直.當燈罩的軸線通過公路路面一側的中間時(除去綠化帶的路面部分),照明效果最理想,問:應設計多高的燈柱,才能取得最理想的照明效果?(精確到0.01m,參考數據$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
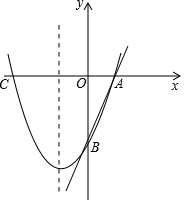 如圖,已知直線y=3x-3分別交x軸、y軸于A、B兩點,拋物線y=x2+bx+c經過
如圖,已知直線y=3x-3分別交x軸、y軸于A、B兩點,拋物線y=x2+bx+c經過查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{\frac{4}{25}}=±\frac{2}{5}$ | B. | $\sqrt{{{({-3})}^2}}=-3$ | C. | -a2沒有平方根 | D. | $-\sqrt{{{({-4})}^2}}=-4$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com