
【題目】某商場(chǎng)經(jīng)調(diào)研得出某種商品每天的利潤(rùn)y(元)與銷(xiāo)售單價(jià)x(元)之間滿(mǎn)足關(guān)系:y=ax2+bx﹣75,其圖象如圖所示.
(1)求a與b的值;
(2)銷(xiāo)售單價(jià)為多少元時(shí),該種商品每天的銷(xiāo)售利潤(rùn)最大?最大利潤(rùn)是多少元?(參考公式:當(dāng)x=![]() 時(shí),二次函數(shù)y=ax2+bx+c(a≠0)有最小(大)值)
時(shí),二次函數(shù)y=ax2+bx+c(a≠0)有最小(大)值)
(3)銷(xiāo)售單價(jià)定在多少時(shí),該種商品每天的銷(xiāo)售利潤(rùn)為21元?結(jié)合圖象,直接寫(xiě)出銷(xiāo)售單價(jià)定在什么范圍時(shí),該種商品每天的銷(xiāo)售利潤(rùn)不低于21元?
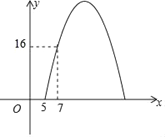
【答案】(1)a=-1 ,b=20;(2)當(dāng)x=10時(shí),y值最大,最大值為25.即銷(xiāo)售單價(jià)定為10元時(shí),銷(xiāo)售利潤(rùn)最大,為25元;(3)銷(xiāo)售單價(jià)在8 ≤x ≤12時(shí),銷(xiāo)售利潤(rùn)不低于21元.
【解析】
(1)利用待定系數(shù)法求二次函數(shù)解析式得出即可;
(2)利用配方法求出二次函數(shù)最值即可;
(3)根據(jù)題意令y=21,解方程可得x的值,結(jié)合圖象可知x的范圍.
(1)y=ax2+bx-75圖象過(guò)點(diǎn)(5,0)、(7,16),
∴![]() ,
,
解得:![]() ;
;
(2)∵y=-x2+20x-75=-(x-10)2+25,
∴當(dāng)x=10時(shí),y最大=25.
答:銷(xiāo)售單價(jià)為10元時(shí),該種商品每天的銷(xiāo)售利潤(rùn)最大,最大利潤(rùn)為25元;
(3)根據(jù)題意,當(dāng)y=21時(shí),得:-x2+20x-75=21,
解得:x1=8,x2=12,
∴x=8或x=12即銷(xiāo)售單價(jià)定在8元或12元時(shí),該種商品每天的銷(xiāo)售利潤(rùn)為21元;
故銷(xiāo)售單價(jià)在8≤x≤12時(shí),銷(xiāo)售利潤(rùn)不低于21元.


 通城學(xué)典默寫(xiě)能手系列答案
通城學(xué)典默寫(xiě)能手系列答案 金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
金牌教輔培優(yōu)優(yōu)選卷期末沖刺100分系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知AB是⊙O的直徑,弦CD與AB相交,∠BAC=38°.
(1)如圖①,若D為弧AB的中點(diǎn),求∠ABC和∠ABD的大小;
(2)如圖②,過(guò)點(diǎn)D作⊙O的切線(xiàn),與AB的延長(zhǎng)線(xiàn)交于點(diǎn)P,若DP∥AC,求∠OCD的大小.
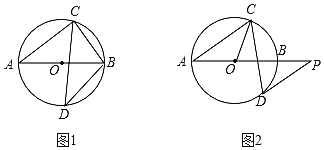
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
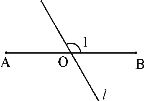
【題目】如圖,AB=6,O是AB的中點(diǎn),直線(xiàn)l經(jīng)過(guò)點(diǎn)O,∠1=120°,P是直線(xiàn)l上一點(diǎn)。當(dāng)△APB為直角三角形時(shí),AP= .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,四邊形ABCD為正方形.點(diǎn)A的坐標(biāo)為(0,2),點(diǎn)B的坐標(biāo)為(0,﹣3),反比例函數(shù)![]()
![]() 的圖象經(jīng)過(guò)點(diǎn)C.
的圖象經(jīng)過(guò)點(diǎn)C.
(1)求反比例函數(shù)的解析式;
(2)若點(diǎn)P是反比例函數(shù)圖象上的一點(diǎn),△PAD的面積恰好等于正方形ABCD的面積,求點(diǎn)P的坐標(biāo).

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
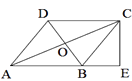
【題目】如圖,在四邊形ABCD中,AB∥DC,AB=AD,對(duì)角線(xiàn)AC、BD相交于點(diǎn)O,AC平分∠BAD,過(guò)點(diǎn)C作CE⊥AB交AB的延長(zhǎng)線(xiàn)于點(diǎn)E,若AB=![]() ,BD=2,則OE的長(zhǎng)等于________.
,BD=2,則OE的長(zhǎng)等于________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
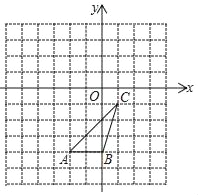
【題目】如圖,在平面直角坐標(biāo)系中,已知A(﹣2,﹣4)、B(0,﹣4)、C(1,﹣1)
(1)畫(huà)出△ABC繞O點(diǎn)逆時(shí)針旋轉(zhuǎn)90°后的圖形△A1B1C1,并寫(xiě)出C1的坐標(biāo);
(2)將(1)中所得△A1B1C1先向左平移4個(gè)單位,再向上平移2個(gè)單位得到△A2B2C2,畫(huà)出△A2B2C2,則C2( , )
(3)若△A2B2C2可以看作△ABC繞某點(diǎn)旋轉(zhuǎn)得來(lái),則旋轉(zhuǎn)中心的坐標(biāo)為 .
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知拋物線(xiàn)![]() .
.
![]() 求該拋物線(xiàn)的對(duì)稱(chēng)軸和頂點(diǎn)P的坐標(biāo).
求該拋物線(xiàn)的對(duì)稱(chēng)軸和頂點(diǎn)P的坐標(biāo).
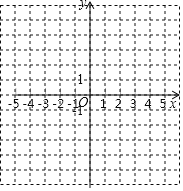
![]() 在圖中的直角坐標(biāo)系內(nèi)用五點(diǎn)法畫(huà)出該拋物線(xiàn)的圖象.
在圖中的直角坐標(biāo)系內(nèi)用五點(diǎn)法畫(huà)出該拋物線(xiàn)的圖象.
![]() 將該拋物線(xiàn)向下平移2個(gè)單位,向左平移3個(gè)單位得到拋物線(xiàn)
將該拋物線(xiàn)向下平移2個(gè)單位,向左平移3個(gè)單位得到拋物線(xiàn)![]() ,此時(shí)點(diǎn)P的對(duì)應(yīng)點(diǎn)為
,此時(shí)點(diǎn)P的對(duì)應(yīng)點(diǎn)為![]() ,試求直線(xiàn)
,試求直線(xiàn)![]() 與y軸的交點(diǎn)坐標(biāo).
與y軸的交點(diǎn)坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
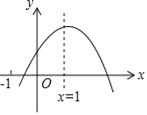
【題目】已知二次函數(shù)y=ax2+bx+c的圖象如圖所示,給出下列結(jié)論:①abc>0;②a﹣b+c<0;③2a+b﹣c<0;④4a+2b+c>0,⑤若點(diǎn)(﹣![]() ,y1)和(
,y1)和(![]() ,y2)在該圖象上,則y1>y2.其中正確的結(jié)論是_____(填入正確結(jié)論的序號(hào))
,y2)在該圖象上,則y1>y2.其中正確的結(jié)論是_____(填入正確結(jié)論的序號(hào))
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】四位同學(xué)在研究函數(shù)y=x2+bx+c(b,c是常數(shù))時(shí),甲發(fā)現(xiàn)當(dāng)x=1時(shí),函數(shù)有最小值;乙發(fā)現(xiàn)﹣1是方程x2+bx+c=0的一個(gè)根;丙發(fā)現(xiàn)函數(shù)的最小值為3;丁發(fā)現(xiàn)當(dāng)x=2時(shí),y=4,已知這四位同學(xué)中只有一位發(fā)現(xiàn)的結(jié)論是錯(cuò)誤的,則該同學(xué)是( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com