
【題目】閱讀下面材料:小明遇到這樣一個問題;△ABC中,有兩個內角相等.
①若∠A=110°,求∠B的度數;
②若∠A=40°,求∠B的度數.
小明通過探究發現,∠A的度數不同,∠B的度數的個數也可能不同,因此為同學們提供了如下解題的想法:
對于問題①,根據三角形內角和定理,∵∠A=110°>90°,∠B=∠C=35°;
對于問題②,根據三角形內角和定理,∵∠A=40°<90°,∴∠A=∠B或∠A=∠C或∠B=∠C,∴∠B的度數可求.請回答:
(1)問題②中∠B的度數為 ;
(2)參考小明解決問題的思路,解決下面問題:
△ABC中,有兩個內角相等.設∠A=x°,當∠B有三個不同的度數時,求∠B的度數(用含x的代式表示)以及x的取值范圍.
【答案】(1)40°或70°或100°;(2)∠B=x°或180°﹣2x°或90°﹣![]() x°,x的取值范圍是0<x<90且x≠60.
x°,x的取值范圍是0<x<90且x≠60.
【解析】
(1)根據三角形內角和定理即可求出答案.
(2)由(1)問的解答過程可類比求出x的取值范圍.
解:(1)當∠A=∠B時,
∴∠B=40°,
當∠A=∠C=40°時,
∴∠B=180﹣∠A﹣∠C=100°,
當∠B=∠C時,
∴![]()
故∠B的度數為40°或70°或100°
(2)當0<x<90時,∠B的度數有三個,
當∠A=∠B時,∠B=x°,
當∠A=∠C時,
∵∠A+∠B+∠C=180°,
∴∠B=180﹣2x°,
當∠B=∠C時,
∵∠A+∠B+∠C=180°,
∴![]()
∵![]()
∴x≠60
∴∠B=x°或180°﹣2x°或![]()
x的取值范圍是0<x<90且x≠60


科目:初中數學 來源: 題型:
【題目】如圖①所示,已知,BC∥OA,∠B=∠A=100°,試解答下列問題:
(1)試說明:OB∥AC;

(2)如圖②,若點E.F在BC上,且∠FOC=∠AOC,OE平分∠BOF.試求∠EOC的度數;

(3)在(2)小題的條件下,若左右平行移動AC,如圖③,那么∠OCB:∠OFB的比值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.

(4)在(3)小題的條件下,當∠OEB=∠OCA時,試求∠OCA的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABOC中,∠A=60°,它的一個頂點C在反比例函數y= ![]() 的圖象上,若將菱形向下平移2個單位,點A恰好落在函數圖象上,則反比例函數解析式為( )
的圖象上,若將菱形向下平移2個單位,點A恰好落在函數圖象上,則反比例函數解析式為( )
A.y=﹣ ![]()
B.y=﹣ ![]()
C.y=﹣ ![]()
D.y= ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,ABCD的頂點A、B的坐標分別是A(﹣1,0),B(0,﹣2),頂點C、D在雙曲線y= ![]() 上,邊AD交y軸于點E,且四邊形BCDE的面積是△ABE面積的5倍,則k= .
上,邊AD交y軸于點E,且四邊形BCDE的面積是△ABE面積的5倍,則k= . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的中線,E,F為直線AD上的點,連接BE,CF,且BE∥CF.
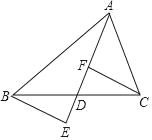
(1)求證:DE=DF;
(2)若在原有條件基礎上再添加AB=AC,你還能得出什么結論.(不用證明)(寫2個)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖示二次函數y=ax2+bx+c的對稱軸在y軸的右側,其圖象與x軸交于點A(﹣1,0)與點C(x2 , 0),且與y軸交于點B(0,﹣2),小強得到以下結論:①0<a<2;②﹣1<b<0;③c=﹣1;④當|a|=|b|時x2> ![]() ﹣1;以上結論中正確結論的序號為 .
﹣1;以上結論中正確結論的序號為 . 
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射線
是射線![]() 上一點,連接
上一點,連接![]() ,沿
,沿![]() 將
將![]() 折疊,得
折疊,得![]() .
.
(1)如圖所示,當![]() 時,
時,![]() _______度;
_______度;

(2)如圖所示,當![]() 時,求線段
時,求線段![]() 的長度;
的長度;

(3)當點![]() 為
為![]() 中點時,點
中點時,點![]() 是邊
是邊![]() 上不與點
上不與點![]() 、
、![]() 重合的一個動點,將
重合的一個動點,將![]() 沿
沿![]() 折疊,得到
折疊,得到![]() ,連接
,連接![]() ,求
,求![]() 周長的最小值.
周長的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com