
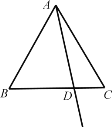
【題目】在△ABC中,AB>BC,直線l垂直平分AC.

(1)如圖1,作∠ABC的平分線交直線l于點D,連接AD,CD.
①補全圖形;
②判斷∠BAD和∠BCD的數量關系,并證明.
(2)如圖2,直線l與△ABC的外角∠ABE的平分線交于點D,連接AD,CD.求證:∠BAD=∠BCD.
【答案】(1)①見解析;②∠BAD+∠BCD=180°,證明見解析;(2)見解析.
【解析】
(1)①根據題意畫圖即可補全圖形;
②過點D作DE⊥AB于點E、DF⊥BC交BC的延長線于點F,如圖4,根據角平分線的性質和線段垂直平分線的性質可得DE=DF,DA=DC,再根據HL可證Rt△ADE≌Rt△CDF,進而可得∠BAD=∠DCF,進一步即可得出∠BAD和∠BCD的數量關系;
(2)過點D作DH⊥AB于點H,DG⊥CE于點G,如圖5,根據角平分線的性質和線段垂直平分線的性質可得DG=DH,DA=DC,再根據HL可證Rt△ADH≌Rt△CDG,進一步即可得出結論.
解:(1)①補全圖形如圖3;
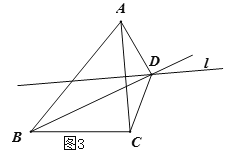
②∠BAD+∠BCD=180°.
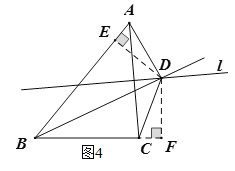
證明:過點D作DE⊥AB于點E、DF⊥BC交BC的延長線于點F,如圖4,
∵BD平分∠ABC,∴DE=DF,
∵直線l垂直平分AC,∴DA=DC,
∴Rt△ADE≌Rt△CDF(HL),∴∠BAD=∠DCF,
∵∠DCF+∠BCD=180°,
∴∠BAD+∠BCD=180°;
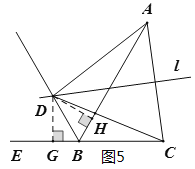
(3)證明:過點D作DH⊥AB于點H,DG⊥CE于點G,如圖5,
∵BD平分∠ABE,∴DH=DG,
∵直線l垂直平分AC,∴DA=DC,
∴Rt△ADH≌Rt△CDG(HL),
∴∠BAD=∠BCD,


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
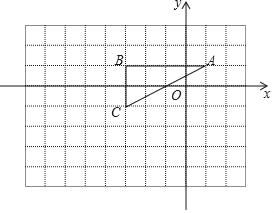
【題目】如圖所示,在平面直角坐標系中有一格點三角形,該三角形的三個頂點為:A(1,1),B(﹣3,1),C(﹣3,﹣1).
(1)若△ABC的外接圓的圓心為P,則點P的坐標為_____,⊙P的半徑為_____;
(2)如圖所示,在11×8的網格圖內,以坐標原點O點為位似中心,將△ABC按相似比2:1放大,A、B、C的對應點分別為A'、B'、C'.①畫出△A'B'C';②將△A'B'C'沿x軸方向平移,需平移_____個單位長度,能使得B'C'所在的直線與⊙P相切.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖為兩正方形ABCD、CEFG和矩形DFHI的位置圖,其中D,A兩點分別在CG、BI上,若AB=3,CE=5,則矩形DFHI的面積是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(問題背景)
如圖,在平面直角坐標系![]() 中,點
中,點![]() 的坐標是
的坐標是![]() ,點
,點![]() 是
是![]() 軸上的一個動點.當點
軸上的一個動點.當點![]() 在
在![]() 軸上移動時,始終保持
軸上移動時,始終保持![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() (點
(點![]() 、
、![]() 、
、![]() 按逆時針方向排列);當點
按逆時針方向排列);當點![]() 移動到點
移動到點![]() 時,得到等腰直角三角形
時,得到等腰直角三角形![]() (此時點
(此時點![]() 與點
與點![]() 重合).
重合).
(初步探究)
(1)寫出點![]() 的坐標______.
的坐標______.
(2)點![]() 在
在![]() 軸上移動過程中,當等腰直角三角形
軸上移動過程中,當等腰直角三角形![]() 的頂點
的頂點![]() 在第四象限時,連接
在第四象限時,連接![]() .
.
求證:![]() ;
;
(深入探究)
(3)當點![]() 在
在![]() 軸上移動時,點
軸上移動時,點![]() 也隨之運動.經過探究發現,點
也隨之運動.經過探究發現,點![]() 的橫坐標總保持不變,請直接寫出點
的橫坐標總保持不變,請直接寫出點![]() 的橫坐標:______.
的橫坐標:______.
(拓展延伸)
(4)點![]() 在
在![]() 軸上移動過程中,當
軸上移動過程中,當![]() 為等腰三角形時,直接寫出此時點
為等腰三角形時,直接寫出此時點![]() 的坐標.
的坐標.
 備用圖
備用圖
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程(k﹣1)x2﹣2kx+k+2=0有兩個不相等的實數根.
(1)求k的取值范圍;
(2)若x1,x2是一元二次方程的兩個實數根,且滿足![]() =﹣2,求k的值,并求此時方程的解.
=﹣2,求k的值,并求此時方程的解.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,AD平分∠BAC交BC于D,∠MDN的兩邊分別與AB,AC相交于M,N兩點,且DM=DN.
(1)如圖甲,若∠C=90°,∠BAC=60°,AC=9,∠MDN=120°,ND∥AB.
①寫出∠MDA= °,AB的長是 .
②求四邊形AMDN的周長;

(2)如圖乙,過D作DF⊥AC于F,先補全圖乙再證明AM+AN=2AF.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等邊△ABC 中,點 D 是線段 BC 上一點.作射線 AD ,點 B 關于射線 AD 的對稱點為 E .連接 EC 并延長,交射線 AD 于點 F .
(1)補全圖形;(2)求∠AFE 的度數;(3)用等式表示線段 AF 、CF 、 EF 之間的數量關系,并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系中的任意兩點![]() ,
,![]() ,我們把
,我們把![]() 叫
叫![]() ,
,![]() 兩點間的“平面距離”,記作
兩點間的“平面距離”,記作![]() .
.
(![]() )已知
)已知![]() 為坐標原點,動點
為坐標原點,動點![]() 是坐標軸上的點,滿足
是坐標軸上的點,滿足![]() ,請寫出點
,請寫出點![]() 的坐標.答:__________.
的坐標.答:__________.
(![]() )設
)設![]() 是平面上一點,
是平面上一點,![]() 是直線
是直線![]() 上的動點,我們定義
上的動點,我們定義![]() 的最小值叫做
的最小值叫做![]() 到直線
到直線![]() 的“平面距離”.試求點
的“平面距離”.試求點![]() 到直線
到直線![]() 的“平面距離”.
的“平面距離”.
(![]() )在上面的定義基礎上,我們可以定義平面上一條直線
)在上面的定義基礎上,我們可以定義平面上一條直線![]() 與⊙
與⊙![]() 的“直角距離”:在直線
的“直角距離”:在直線![]() 與⊙
與⊙![]() 上各自任取一點,此兩點之間的“平面距離”的最小值稱為直線
上各自任取一點,此兩點之間的“平面距離”的最小值稱為直線![]() 與⊙
與⊙![]() 的“平面距離”,記作
的“平面距離”,記作![]() .
.
試求直線![]() 與圓心在直線坐標系原點、半徑是
與圓心在直線坐標系原點、半徑是![]() 的⊙
的⊙![]() 的直角距離
的直角距離![]() __________.(直接寫出答案)
__________.(直接寫出答案)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙、丙三位運動員在相同條件下各射靶![]() 次,每次射靶的成績如下:
次,每次射靶的成績如下:
甲:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
乙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
丙:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
(1)根據以上數據完成下表:
平均數 | 中位數 | 方差 | |
甲 |
|
| __________ |
乙 | __________ |
|
|
丙 |
| __________ |
|
(2)根據表中數據分析,哪位運動員的成績最穩定.并簡要說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com