Question

已知拋物線y＝ax²＋bx＋c經(jīng)過A(－1，0)、B(3，0)、C(0，3)三點，直線l是拋物線的對稱軸．

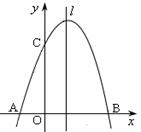(1)求拋物線的解析式和對稱軸；      

(2)設(shè)點P是直線l上的一個動點，當△PAC是以AC為斜邊的Rt△時，求點P的坐標；

(3)在直線l上是否存在點M，使△MAC為等腰三角形？若存在，求出點M的坐標；若不存在，請說明理由；

(4)設(shè)過點A的直線與拋物線在第一象限的交點為N，當△ACN的面積為時，求直線AN的解析式.

Answer 1

解：（1）設(shè)拋物線解析式為：

對稱軸為：直線

（注：對稱軸未寫直線二字不扣分）

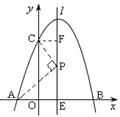（2）設(shè)點P（1，y）是直線l上的一個動點，作CF⊥l于F，l交x軸于E，

則AC²＝AO²＋CO²＝10，CP²＝CF²＋PF²＝1＋（3－y）²＝

AP²＝AE²＋PE²＝4＋y², ∴由CP²＋AP²＝AC²，

得：＋4＋y²＝10，解得或

∴P點的坐標為P₁（1，1）、P₂（1, 2）

（說明: 求得一個點1分、2個點3分，求解過程不必要求過細，看結(jié)果為主）

（解法二 用△相似解法更簡單如下：

∵CP⊥AP，∴△CPF∽△PAE，∴，∴∴解得或 同樣給分）

（3）設(shè)點M（1，m）, 與（2）同理可得：AC²＝10，CM²＝，AM²＝4＋m²

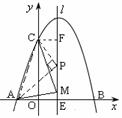①當AC＝CM時，10＝，解得：m＝0或m＝6（舍去）

②當AC＝AM時，10＝4＋m², 解得：m＝或m＝

③當CM＝AM時，＝4＋m²，解得：m＝1

檢驗：當m＝6時，M、A、C三點共線，不合題意，故舍去；

綜上可知，符合條件的M點有4個，

M坐標為(1，0) 、(1，)、(1，－)、(1，1)

（注：求出5個點，未舍去(1，6)，不扣分）

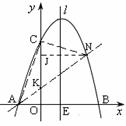
(4) 設(shè)直線AN的解析式為，且交y軸于點K，∵過點A（—1, 0），∴，

∴K（0，k），∵N是直線AN與拋物線的交點，∴，解得x＝3—k，

或x＝—1（舍去），∴N點的橫坐標為x＝3—k （k＜3）  

由S_△ACN＝S_△ACK＋S_△CKN＝CK·OA＋CK·NJ＝（3—k）×1＋（3—k）²

＝ 令＝，解得k＝（舍去），或k＝，

∴直線AN的解析式為