
【題目】已知二次函數y=(m﹣2)x2+2mx+m﹣3的圖象與x軸有兩個交點,(x1,0),(x2,0),則下列說法正確是( )
①該函數圖象一定過定點(﹣1,﹣5);
②若該函數圖象開口向下,則m的取值范圍為:![]() m<2;
m<2;
③當m>2,且1≤x≤2時,y的最大值為:4m﹣5;
④當m>2,且該函數圖象與x軸兩交點的橫坐標x1,x2滿足﹣3<x1<﹣2,﹣1<x2<0時,m的取值范圍為:![]() m<11.
m<11.
A.①②③④B.①②④C.①③④D.②③④
【答案】B
【解析】
①把二次函數整理成合適的形式,再把點(﹣1,﹣5)代入即可判斷正誤;
②由函數圖象開口向下可知,二次項系數小于0,即m﹣2<0,且根的判別式大于0,即△=b2﹣4ac=20m﹣24>0,解不等式即可求解;
③由m>2,可知二次函數開口向上,再判斷函數的對稱軸的位置,再根據函數增減性即可判斷;
④根據開口向上的二次函數與x軸交點的特點可得關于m的不等式,解不等式即可判斷.
①y=(m﹣2)x2+2mx+m﹣3=m(x+1)2﹣2x2﹣3,
當x=﹣1時,y=﹣5,故該函數圖象一定過定點(﹣1,﹣5),符合題意;
②若該函數圖象開口向下,則m﹣2<0,且△>0,
△=b2﹣4ac=20m﹣24>0,解得:m![]() ,且m<2,故m的取值范圍為:
,且m<2,故m的取值范圍為:![]() m<2,符合題意;
m<2,符合題意;
③當m>2,m-2>0,即二次函數開口向上,對稱軸x=![]() =
=![]() =
=![]() <
<![]() ,函數的對稱軸在﹣1的左側,則當1≤x≤2時,y隨x的增加而增大,在x=2時,y取得最大值,y的最大為:4 (m-2)+4m+m-3=9m-11,故原答案錯誤,不符合題意;
,函數的對稱軸在﹣1的左側,則當1≤x≤2時,y隨x的增加而增大,在x=2時,y取得最大值,y的最大為:4 (m-2)+4m+m-3=9m-11,故原答案錯誤,不符合題意;
④當m>2,x=﹣3時,y=9(m﹣2)﹣6m+m﹣3=4m﹣21,當x=﹣2時,y=m﹣11,當﹣3<x1<﹣2時,則(4m﹣21)(m﹣11)<0,解得:![]() m<11;
m<11;
同理﹣1<x2<0時,m>3,故m的取值范圍為:![]() m<11正確,符合題意.
m<11正確,符合題意.
故選:B.


 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案 黃岡課堂作業本系列答案
黃岡課堂作業本系列答案科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() ,與x軸交于A、B兩點(點A在點B的左側).
,與x軸交于A、B兩點(點A在點B的左側).
(1)求點A和點B的坐標;
(2)若點P(m,n)是拋物線上的一點,過點P作x軸的垂線,垂足為點D.
①在![]() 的條件下,當
的條件下,當![]() 時,n的取值范圍是
時,n的取值范圍是![]() ,求拋物線的表達式;
,求拋物線的表達式;
②若D點坐標(4,0),當![]() 時,求a的取值范圍.
時,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,AC,BD交于點O,且AO=BO.
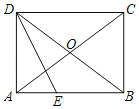
(1)求證:四邊形ABCD是矩形;
(2)∠ADB的角平分線DE交AB于點E,當AD=3,tan∠CAB=![]() 時,求AE的長.
時,求AE的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,點
中,點![]() ,若射線
,若射線![]() 上存在點
上存在點![]() ,使得
,使得![]() 是以
是以![]() 為腰的等腰三角形,就稱點
為腰的等腰三角形,就稱點![]() 為線段
為線段![]() 關于射線
關于射線![]() 的等腰點.
的等腰點.
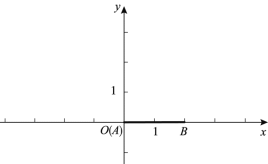
(1)如圖, ![]() ,
,
①若![]() ,則線段
,則線段![]() 關于射線
關于射線![]() 的等腰點的坐標是_____;
的等腰點的坐標是_____;
②若![]() ,且線段
,且線段![]() 關于射線
關于射線![]() 的等腰點的縱坐標小于1,求
的等腰點的縱坐標小于1,求![]() 的取值范圍;
的取值范圍;
(2) 若![]() ,且射線
,且射線![]() 上只存在一個線段
上只存在一個線段![]() 關于射線
關于射線![]() 的等腰點,則
的等腰點,則![]() 的取值范圍是__________.
的取值范圍是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
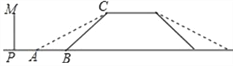
【題目】某地的一座人行天橋如圖所示,天橋高為6米,坡面BC的坡度為1:1,為了方便行人推車過天橋,有關部門決定降低坡度,使新坡面的坡度為1:![]() .
.
(1)求新坡面的坡角∠CAB的度數;
(2)原天橋底部正前方8米處(PB的長)的文化墻PM是否需要拆除?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據學習函數的經驗,探究函數y=x2+ax﹣4|x+b|+4(b<0)的圖象和性質:
(1)下表給出了部分x,y的取值;
x | L | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 | L |
y | L | 3 | 0 | ﹣1 | 0 | 3 | 0 | ﹣1 | 0 | 3 | L |
由上表可知,a= ,b= ;
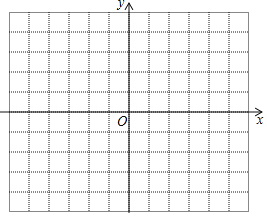
(2)用你喜歡的方式在坐標系中畫出函數y=x2+ax﹣4|x+b|+4的圖象;
(3)結合你所畫的函數圖象,寫出該函數的一條性質;
(4)若方程x2+ax﹣4|x+b|+4=x+m至少有3個不同的實數解,請直接寫出m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人進行摸牌游戲,現有三張形狀大小完全相同的牌,正面分別標有數字![]() ,
,![]() ,
,![]() ,將三張牌背面朝上,洗勻后放在桌子上.
,將三張牌背面朝上,洗勻后放在桌子上.
(1)甲從中隨機抽取一張牌,記錄數字后放回洗勻,乙再隨機抽取一張.請用列表法或畫樹狀圖的方法寫出所有可能的結果;
(2)若兩人抽取的數字和為![]() 的倍數,則甲獲勝;若抽取的數字和為
的倍數,則甲獲勝;若抽取的數字和為![]() 的倍數,則乙獲勝,這個游戲公平嗎?請用概率的知識加以解釋.
的倍數,則乙獲勝,這個游戲公平嗎?請用概率的知識加以解釋.
查看答案和解析>>
科目:初中數學 來源: 題型:
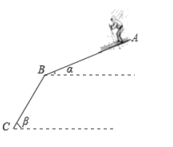
【題目】2022年在北京將舉辦第24屆冬季奧運會,很多學校都開展了冰雪項目學習.如圖,滑雪軌道由AB,BC兩部分組成,AB,BC的長度都為200米,一位同學乘滑雪板沿此軌道由A點滑到了C點,若AB與水平面的夾角α為20°,BC與水平面的夾角β為45°,則他下降的高度為多少米.(結果保留整數)(參考數據sin20°≈0.342,cos20°≈0.940,tan20°≈0.364)
查看答案和解析>>
科目:初中數學 來源: 題型:
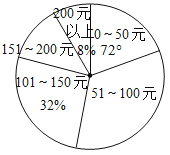
【題目】某社區踴躍為“抗擊肺炎”捐款,根據捐款情況(捐款數為正數)制作以下統計圖表,但工作人員不小心把墨水滴在統計表上,部分數據看不清楚.
(1)共有多少人捐款?
(2)如果捐款0~50元的人數在扇形統計圖中所占的圓心角為72°,那么捐款51~100元的有多少人?
捐款 | 人數 |
0~50元 | |
51~100元 | |
101~150元 | |
151~200元 | 6 |
200元以上 | 4 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com