
【題目】如圖所示,點P是∠ABC內一點.
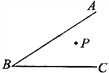
(1)畫圖:①過點P畫BC的垂線,垂足為D;②過點P畫BC的平行線交AB于點E,過點P畫AB的平行線交BC于點F.
(2)∠EPF等于∠B嗎?為什么?
【答案】(1)圖形見解析(2)∠EPF=∠B
【解析】試題分析:(1)①過點P作BC的垂線,D是垂足;②過點P作BC的平行線交AB于E,過點P作AB的平行線交BC于F;
(2)根據平行線的性質可得∠AEP=∠B,∠EPF=∠AEP然后利用等量代換得到結論即可.
解:如圖所示,(1)①直線PD即為所求;②直線PE、PF即為所求.
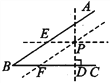
(2)∠EPF=∠B,理由:因為PE∥BC(已知),所以∠AEP=∠B(兩直線平行,同位角相等).又因為PF∥AB(已知),所以∠EPF=∠AEP(兩直線平行,內錯角相等),∠EPF=∠B(等量代換).
點睛:本題考查了平行線和垂線的畫法及平行線的性質,熟練掌握兩直線平行同位角相等,兩直線平行內錯角相等是解答本題的關鍵.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠B=30°,以A為圓心,任意長為半徑畫弧分別交AB、AC于點M和N,再分別以M、N為圓心,大于![]() MN的長為半徑畫弧,兩弧交于點P,連接AP,并延長交BC于點D,則下列說法中正確的個數是( )
MN的長為半徑畫弧,兩弧交于點P,連接AP,并延長交BC于點D,則下列說法中正確的個數是( )

①AD是∠BAC的平分線;②∠ADC=60°;③點D在AB的垂直平分線上;④若AC=![]() dm,AD=2dm,則點D到AB的距離是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
dm,AD=2dm,則點D到AB的距離是1dm;⑤S△DAC∶S△DAB=AC∶AB=1∶2
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
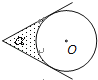
【題目】如圖,⊙O的圓心在定角∠α(0°<α<180°)的角平分線上運動,且⊙O與∠α的兩邊相切,圖中陰影部分的面積S關于⊙O的半徑r(r>0)變化的函數圖象大致是( )
A. 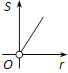 B.
B. 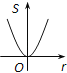 C.
C. 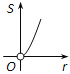 D.
D. 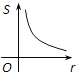
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 的對角線
的對角線![]() ,
, ![]() 相交于點
相交于點![]() ,
, ![]() 關于
關于![]() 的對稱圖形為
的對稱圖形為![]() .
.

(1)求證:四邊形![]() 是菱形;
是菱形;
(2)連接![]() ,若
,若![]() ,
, ![]() .
.
①求![]() 的值;
的值;
②若點![]() 為線段
為線段![]() 上一動點(不與點
上一動點(不與點![]() 重合),連接
重合),連接![]() ,一動點
,一動點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度沿線段
的速度沿線段![]() 勻速運動到點
勻速運動到點![]() ,再以
,再以![]() 的速度沿線段
的速度沿線段![]() 勻速運動到點
勻速運動到點![]() ,到達點
,到達點![]() 后停止運動.當點
后停止運動.當點![]() 沿上述路線運動到點
沿上述路線運動到點![]() 所需要的時間最短時,求
所需要的時間最短時,求![]() 的長和點
的長和點![]() 走完全程所需的時間.
走完全程所需的時間.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 的面積為1.分別倍長(延長一倍)
的面積為1.分別倍長(延長一倍)![]() ,BC,CA得到
,BC,CA得到![]() .再分別倍長A1B1,B1C1,C1A1得到
.再分別倍長A1B1,B1C1,C1A1得到![]() .…… 按此規律,倍長2018次后得到的
.…… 按此規律,倍長2018次后得到的![]() 的面積為( )
的面積為( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,邊長為2的正方形ABCD關于y軸對稱,邊AD在x軸上,點B在第四象限,直線BD與反比例函數![]() 的圖象交于點B、E.
的圖象交于點B、E.
(1)求反比例函數及直線BD的解析式;
(2)求點E的坐標;
(3)連結![]() 、
、![]() 、
、![]() ,求△
,求△![]() 的面積.
的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:∠MON=80°,OE平分∠MON,點A、B、C分別是射線OM、OE、ON上的動點(A、B、C不與點O 重合),連接AC交射線OE于點D.設∠OAC=x°.
(1)如圖1,若AB∥ON,則:①∠ABO的度數是 ;
②如圖2,當∠BAD=∠ABD時,試求x的值(要說明理由);
(2)如圖3,若AB⊥OM,則是否存在這樣的X的值,使得△ADB中有兩個相等的角?若存在,直接寫出x的值;若不存在,說明理由.(自己畫圖)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() 的三個頂點的坐標分別為
的三個頂點的坐標分別為![]() 、
、![]() 、
、![]() .
.
(1)請直接寫出點![]() 關于
關于![]() 軸對稱的點的坐標;
軸對稱的點的坐標;
(2)將![]() 繞坐標原點
繞坐標原點![]() 逆時針旋轉90°.畫出圖形,直接寫出點
逆時針旋轉90°.畫出圖形,直接寫出點![]() 的對應點的坐標;
的對應點的坐標;
(3)請直接寫出:以![]() 為頂點的平行四邊形的第四個頂點
為頂點的平行四邊形的第四個頂點![]() 的坐標.
的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
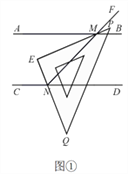
【題目】已知: 兩直線![]() ,
,![]() ,且
,且![]() ∥CD,點
∥CD,點![]() ,
,![]() 分別在直線
分別在直線![]() ,
,![]() 上. 放置一個足夠大的三角尺,使得三角尺的兩邊
上. 放置一個足夠大的三角尺,使得三角尺的兩邊![]() ,
,![]() 分別經過點
分別經過點![]() ,
,![]() . 過點
. 過點![]() 作射線
作射線![]() ,使得
,使得![]() .
.
(1)轉動三角尺,如圖①所示,當射線![]() 與
與![]() 重合,
重合,![]() 時,則
時,則![]() ________;
________;
(2)轉動三角尺,如圖②所示,當射線![]() 與
與![]() 不重合,
不重合,![]() 時,求
時,求![]() 的度數.
的度數.
(3)轉動直角三角尺的過程中, 請直接寫出![]() 與
與![]() 之間的數量關系.
之間的數量關系.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com