
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y= ![]() (k>0)的圖象與BC邊交于點E.
(k>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積為 ![]() .
.
【答案】
(1)
解:∵在矩形OABC中,OA=3,OC=2,
∴B(3,2),
∵F為AB的中點,
∴F(3,1),
∵點F在反比例函數y= ![]() (k>0)的圖象上,
(k>0)的圖象上,
∴k=3,
∴該函數的解析式為y= ![]() ;
;
(2)
解:由題意知E,F兩點坐標分別為E( ![]() ,2),F(3,
,2),F(3, ![]() ),
),
∴S△EFA= ![]() AFBE=
AFBE= ![]() ×
× ![]() k(3﹣
k(3﹣ ![]() k),
k),
= ![]() k﹣
k﹣ ![]() k2
k2
∵△EFA的面積為 ![]() .
.
∴ ![]() k﹣
k﹣ ![]() k2=
k2= ![]() .
.
整理,得
k2﹣6k+8=0,
解得k1=2,k2=4,
∴當k的值為2或4時,△EFA的面積為 ![]() .
.
【解析】(1)當F為AB的中點時,點F的坐標為(3,1),由此代入求得函數解析式即可;(2)根據圖中的點的坐標表示出三角形的面積,得到關于k的方程,通過解方程求得k的值即可.
【考點精析】本題主要考查了反比例函數的圖象和反比例函數的性質的相關知識點,需要掌握反比例函數的圖像屬于雙曲線.反比例函數的圖象既是軸對稱圖形又是中心對稱圖形.有兩條對稱軸:直線y=x和 y=-x.對稱中心是:原點;性質:當k>0時雙曲線的兩支分別位于第一、第三象限,在每個象限內y值隨x值的增大而減小; 當k<0時雙曲線的兩支分別位于第二、第四象限,在每個象限內y值隨x值的增大而增大才能正確解答此題.


 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案科目:初中數學 來源: 題型:
【題目】(1)如圖①,你知道∠BOC=∠B+∠C+∠A的奧秘嗎?請用你學過的知識予以證明;
(2)如圖②,設x=∠A+∠B+∠C+∠D+∠E,運用(1)中的結論填空.
x=____________°;x=____________°;x=____________°;
(3)如圖③,一個六角星,其中∠BOD=70°,則∠A+∠B+∠C+∠D+∠E+∠F=________°.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一次“尋寶”人找到了如圖所示的兩個標志點A(2,3),B(4,1),A,B兩點到“寶藏”點的距離都是![]() ,則“寶藏”點的坐標是( )
,則“寶藏”點的坐標是( )
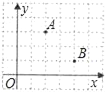
A. (1,0) B. (5,4) C. (1,0)或(5,4) D. (0,1)或(4,5)
查看答案和解析>>
科目:初中數學 來源: 題型:
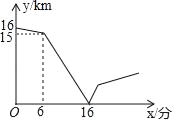
【題目】甲、乙兩人在一條筆直的道路上相向而行,甲騎自行車從A地到B地,乙駕車從B地到A地,他們分別以不同的速度勻速行駛,已知甲先出發6分鐘后,乙才出發,在整個過程中,甲、乙兩人的距離y(km)與甲出發的時間x(分)之間的關系如圖所示.
(1)求甲、乙相遇時,乙所行駛的路程;
(2)當乙到達終點A時,甲還需多少分鐘到達終點B?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2017年3月全國兩會勝利召開,某學校就兩會期間出現頻率最高的熱詞:A.藍天保衛戰,B.不動產保護,C.經濟增速,D.簡政放權等進行了抽樣調查,每個同學只能從中選擇一個“我最關注”的熱詞,如圖是根據調查結果繪制的兩幅不完整的統計圖.請你根據統計圖提供的信息,解答下列問題: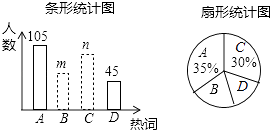
(1)本次調查中,一共調查了名同學;
(2)條形統計圖中,m= , n=;
(3)從該校學生中隨機抽取一個最關注熱詞D的學生的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
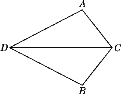
【題目】如圖,點D為碼頭,A,B兩個燈塔與碼頭的距離相等,DA,DB為海岸線,一輪船離開碼頭,計劃沿∠ADB的平分線航行,在航行途中C點處,測得輪船與燈塔A和燈塔B的距離相等.試問:輪船航行是否偏離指定航線?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情境:如圖①,在直角三角形ABC中,∠BAC=90°,AD⊥BC于點D,可知:∠BAD=∠C(不需要證明);
特例探究:如圖②,∠MAN=90°,射線AE在這個角的內部,點B、C在∠MAN的邊AM、AN上,且AB=AC, CF⊥AE于點F,BD⊥AE于點D.證明:△ABD≌△CAF;
歸納證明:如圖③,點BC在∠MAN的邊AM、AN上,點EF在∠MAN內部的射線AD上,∠1、∠2分別是△ABE、△CAF的外角.已知AB=AC, ∠1=∠2=∠BAC.求證:△ABE≌△CAF;
拓展應用:如圖④,在△ABC中,AB=AC,AB>BC.點D在邊BC上,CD=2BD,點E、F在線段AD上,∠1=∠2=∠BAC.若△ABC的面積為15,則△ACF與△BDE的面積之和為 .(12分)




查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=ax2+bx+c(a≠0)的對稱軸為直線x=﹣1,與x軸的一個交點A在點(﹣3,0)和(﹣2,0)之間,其部分圖象如圖所示,則下列4個結論::①b2﹣4ac<0;②2a﹣b=0;③a+b+c<0;④點M(x1 , y1)、N(x2 , y2)在拋物線上,若x1<x2 , 則y1≤y2 , 其中正確結論的個數是( ) 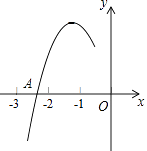
A.1個
B.2個
C.3個
D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:
①ac<0 ②2a+b=0 ③4a+2b+c>0 ④對任意實數x均有ax2+bx≥a+b
正確的結論序號為: . 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com