【題目】如圖，將矩形ABCD繞點A順時針旋轉到矩形A′B′C′D′的位置，旋轉角為α（0°＜α＜90°），若∠1=110°，則∠α= ．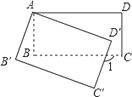
百年學典課時學練測系列答案
仁愛英語同步練習冊系列答案
學習實踐園地系列答案科目：初中數學 來源： 題型：
【題目】閱讀下列一段文字：在直角坐標系中，已知兩點的坐標是M（x1，y1），N（x2，y2）），M，N兩點之間的距離可以用公式MN＝
計算．解答下列問題：
（1）若點P（2，4），Q（﹣3，﹣8），求P，Q兩點間的距離；
（2）若點A（1，2），B（4，﹣2），點O是坐標原點，判斷△AOB是什么三角形，并說明理由．
（3）已知點A(5，5)，B(-4，7)，點P在x軸上，且要使PA+PB的和最小，求PA+PB的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在網格（每個小正方形的邊長均為1）中選取9個格點（格線的交點稱為格點），如果以A為圓心，r為半徑畫圓，選取的格點中除點A外恰好有3個在圓內，則r的取值范圍為（ ）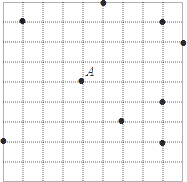
A.2 
＜r＜ 
B. ＜r≤3
C. ＜r＜5
D.5＜r＜ 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB∥CD，∠EBF=2∠ABE，∠EDF=2∠CDE，則∠E與∠F之間滿足的數量關系是（ ）
A. ∠E=∠FB. ∠E＋∠F=180°
C. 3∠E＋∠F=360°D. 2∠E-∠F=90°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠C＝90°，點D是AB邊中點，點E是BC邊上一點，將△ADE沿DE折疊，得到△FDE，使△FDE與△BDE重疊部分的面積是△AEB面積的
，若AC＝3，BC＝6，則線段BE的長為__________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線
與x軸、y軸分別相交于A、B兩點，與直線
交于點C，且點C的橫坐標為1．
（1）求b的值；
（2）點
，
在直線上，若
，則
__________
．
（3）若動點P在線段OC上（點P不與點C重合），連接PA，PB，設點P的橫坐標為m，△PAB的面積為S，求S關于m的函數關系式（不要求寫出自變量m的取值范圍）．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】興華商店準備購進甲、乙兩種書包出售，每個甲種書包的進價比每個乙種書包的進價多20元，購進3個甲種書包的費用和購進4個乙種書包的費用相等，現計劃購進兩種書包共100個，其中乙種書包不少于35個．
（1）甲種書包進價為__________元/個，乙種書包進價為__________元/個；
（2）若甲種書包每個售價120元，乙種書包每個售價90元，且購進這100個書包的費用不低于7200元，如果這100個書包都可售完，那么興華商店如何進貨才能獲得最大利潤？最大利潤是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在菱形
中，
．
（1）如圖1，點
為線段
的中點，連接
，
．若
，求線段
的長．
（2）如圖2，
為線段
上一點（不與
，
重合），以
為邊向上構造等邊三角形
，線段
與
交于點
，連接
，
，
為線段的中點．連接
，
判斷與的數量關系，并證明你的結論．
（3）在（2）的條件下，若
，請你直接寫出
的最小值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下面材料
已知：如圖，四邊形ABCD是平行四邊形；
求作：菱形AECF，使點E，F分別在BC，AD上．
小凱的作法如下：
（1）連接AC；
（2）作AC的垂直平分線EF分別交BC，AD于E，F．
（3）連接AE，CF
所以四邊形AECF是菱形．
老師說：“小凱的作法正確”．
回答問題：
已知：在平行四邊形ABCD中，點E、F分別在邊BC、AD上______________________________________________．（補全已知條件）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
