
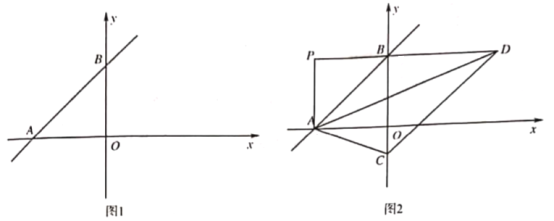
【題目】在平面直角坐標系中,![]() 為坐標原點,直線
為坐標原點,直線![]() 交
交![]() 軸負半軸)軸正半軸于
軸負半軸)軸正半軸于![]() 兩點,
兩點, ![]() 的面積為4.5;
的面積為4.5;
![]() 如圖1.求
如圖1.求![]() 的值;
的值;
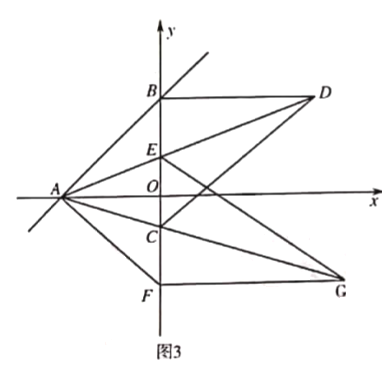
![]() 如圖2.在
如圖2.在![]() 軸負半軸上取點
軸負半軸上取點![]() .點
.點![]() 在第一象限,
在第一象限,![]() 連接
連接![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
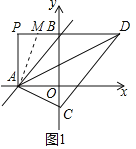
![]() 如圖3,在
如圖3,在![]() 的條件下.
的條件下.![]() 交
交![]() 軸于點
軸于點![]() 軸交
軸交![]() 的延長線于點
的延長線于點![]() ,設
,設![]() 與
與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,當
,當![]() 時,求點
時,求點![]() 的坐標.
的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)分別求![]() 、
、![]() 坐標,其中
坐標,其中![]() 的坐標用
的坐標用![]() 表示,利用
表示,利用![]() 為等量關系即求出
為等量關系即求出![]() 的值.
的值.
(2)由![]() 聯想到在
聯想到在![]() 上截取
上截取![]() ,則有
,則有![]() .由條件易證四邊形
.由條件易證四邊形![]() 是正方形,由
是正方形,由![]() 即得到
即得到![]() ,有
,有![]() ,
,![]() ,通過角度轉換可得
,通過角度轉換可得![]() .證
.證![]() ,即得到
,即得到![]() ,求得
,求得![]() .
.
(3)要求點![]() 坐標,即要求
坐標,即要求![]() 的長,又
的長,又![]() 在
在![]() 中,
中,![]() ,即求出
,即求出![]() 的長則
的長則![]() 確定,即求出
確定,即求出![]() .由
.由![]() 聯想到給
聯想到給![]() 所在的
所在的![]() 構造全等三角形:過點
構造全等三角形:過點![]() 作
作![]() 軸于點
軸于點![]() ,在
,在![]() 上截取
上截取![]() ,連接
,連接![]() ,通過角度轉換可證
,通過角度轉換可證![]() ,即有
,即有![]() .設
.設![]() ,
,![]() ,則能用
,則能用![]() 表示
表示![]() 、
、![]() ,利用勾股定理列方程即求出
,利用勾股定理列方程即求出![]() 的值.求得兩個
的值.求得兩個![]() 的值要分別代入計算討論合理性.
的值要分別代入計算討論合理性.
解:(1)當![]() 時,
時,![]() ,解得:
,解得:![]()
![]() ,
,![]()
當![]() 時,
時,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
(2)在![]() 上截取
上截取![]() ,連接
,連接![]()
![]() 軸,
軸,![]()
![]()
![]() 四邊形
四邊形![]() 是矩形
是矩形
![]() ,
,
![]() ,即
,即![]()
![]() 矩形
矩形![]() 是正方形
是正方形
![]()
在![]() 與
與![]() 中
中
![]()
![]() ,
,![]()
![]()
![]()
![]()
在![]() 與
與![]() 中
中

![]()
![]()
![]()
![]()
(3)過點![]() 作
作![]() 軸于點
軸于點![]() ,在
,在![]() 上截取
上截取![]() ,連接
,連接![]()
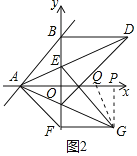
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]() 軸,
軸,![]() 軸
軸
![]() 四邊形
四邊形![]() 是矩形
是矩形
![]() ,
,![]()
在![]() 與
與![]() 中,
中,
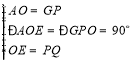
![]()
![]() ,
,![]()
![]()
即![]()
在![]() 與
與![]() 中,
中,

![]()
![]()
設![]() ,則
,則![]()
![]() ,
,![]()
![]()
![]() 在
在![]() 中,
中,![]()
![]()
解得:![]() ,
,![]()
①當![]() 時,
時,![]() ,
,![]()
![]()
![]()
![]()
![]()
②當![]() 時,
時,![]() ,
,![]()
![]()
![]()
![]()
綜上所述,點![]() 坐標為
坐標為![]() 或
或![]()


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=2![]() ,BC=10,E、F分別在邊BC,AD上,BE=DF.將△ABE,△CDF分別沿著AE,CF翻折后得到△AGE,△CHF.若AG、CH分別平分∠EAD、∠FCB,則GH長為( )
,BC=10,E、F分別在邊BC,AD上,BE=DF.將△ABE,△CDF分別沿著AE,CF翻折后得到△AGE,△CHF.若AG、CH分別平分∠EAD、∠FCB,則GH長為( )

A.3B.4C.5D.7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為
為![]() 邊上的動點(點
邊上的動點(點![]() 不與點
不與點![]() ,
,![]() 重合).以
重合).以![]() 為頂點作
為頂點作![]() ,射線
,射線![]() 交
交![]() 邊于點
邊于點![]() ,過點
,過點![]() 作
作![]() 交射線
交射線![]() 于點
于點![]() ,連接
,連接![]() .
.
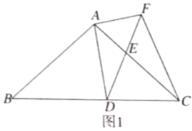
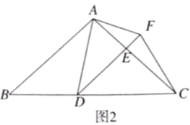
(1)求證:![]() ;
;
(2)當![]() 時(如圖2),求
時(如圖2),求![]() 的長;
的長;
(3)點![]() 在
在![]() 邊上運動的過程中,是否存在某個位置,使得
邊上運動的過程中,是否存在某個位置,使得![]() ?若存在,求出此時
?若存在,求出此時![]() 的長;若不存在,請說明理由.
的長;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,0為原點,A(4,0),E(0,3),四邊形OABC,四邊形OCDE都為平行四邊形,OC=5,函數y=![]() (x>0)的圖象經過AB的中點F和DE的中點G,則k的值為 .
(x>0)的圖象經過AB的中點F和DE的中點G,則k的值為 .
查看答案和解析>>
科目:初中數學 來源: 題型:
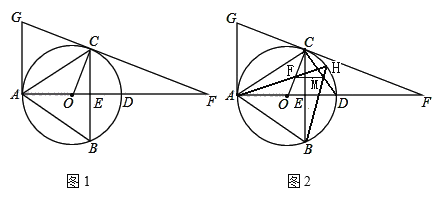
【題目】如圖1,△ABC內接于⊙O,直徑AD交BC于點E,延長AD至點F,使DF=2OD,連接FC并延長交過點A的切線于點G,且滿足AG∥BC,連接OC,若cos∠BAC=![]() ,BC=8.
,BC=8.
(1)求證:CF是⊙O的切線;
(2)求⊙O的半徑OC;
(3)如圖2,⊙O的弦AH經過半徑OC的中點F,連結BH交弦CD于點M,連結FM,試求出FM的長和△AOF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年平昌冬奧會在2月9日到25日在韓國平昌郡舉行,為了調查中學生對冬奧會比賽項目的了解程度,某中學在學生中做了一次抽樣調查,調查結果共分為四個等級:A、非常了解B、比較了解C、基本了解D、不了解.根據調查統計結果,繪制了如圖所示的不完整的三種統計圖表.
對冬奧會了解程度的統計表
對冬奧會的了解程度 | 百分比 |
A非常了解 | 10% |
B比較了解 | 15% |
C基本了解 | 35% |
D不了解 | n% |
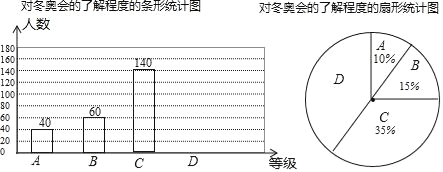
(1)n= ;
(2)扇形統計圖中,D部分扇形所對應的圓心角是 ;
(3)請補全條形統計圖;
(4)根據調查結果,學校準備開展冬奧會的知識競賽,某班要從“非常了解”程度的小明和小剛中選一人參加,現設計了如下游戲來確定誰參賽,具體規則是:把四個完全相同的乒乓球標上數字1,2,3,4然后放到一個不透明的袋中,一個人先從袋中摸出一個球,另一人再從剩下的三個球中隨機摸出一個球,若摸出的兩個球上的數字和為偶數,則小明去,否則小剛去,請用畫樹狀圖或列表的方法說明這個游戲是否公平.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在水果銷售旺季,某水果店購進一優質水果,進價為20元/千克,售價不低于20元/千克,且不超過32元/千克,根據銷售情況,發現該水果一天的銷售量y(千克)與該天的售價x(元/千克)滿足如下表所示的一次函數關系.
銷售量y(千克) | … | 34.8 | 32 | 29.6 | 28 | … |
售價x(元/千克) | … | 22.6 | 24 | 25.2 | 26 | … |
(1)某天這種水果的售價為23.5元/千克,求當天該水果的銷售量.
(2)如果某天銷售這種水果獲利150元,那么該天水果的售價為多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com