
【題目】如圖,在△ABC中,AB=AC,AE是∠BAC的平分線,∠ABC的平分線 BM交AE于點M,點O在AB上,以點O為圓心,OB的長為半徑的圓經過點M,交BC于點G,交AB于點F.
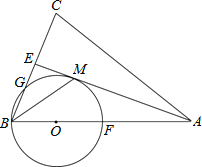
(1)求證:AE為⊙O的切線.
(2)當BC=8,AC=12時,求⊙O的半徑.
(3)在(2)的條件下,求線段BG的長.
【答案】(1)見解析;(2)3;(3)2
【解析】
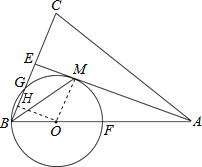
試題分析:(1)連接OM.利用角平分線的性質和平行線的性質得到AE⊥OM后即可證得AE是⊙O的切線;
(2)設⊙O的半徑為R,根據OM∥BE,得到△OMA∽△BEA,利用平行線的性質得到![]() =
=![]() ,即可解得R=3,從而求得⊙O的半徑為3;
,即可解得R=3,從而求得⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,根據∠OME=∠MEH=∠EHO=90°,得到四邊形OMEH是矩形,從而得到HE=OM=3和BH=1,證得結論BG=2BH=2.
(1)證明:連接OM.
∵AC=AB,AE平分∠BAC,
∴AE⊥BC,CE=BE=![]() BC=4,
BC=4,
∵OB=OM,
∴∠OBM=∠OMB,
∵BM平分∠ABC,
∴∠OBM=∠CBM,
∴∠OMB=∠CBM,
∴OM∥BC
又∵AE⊥BC,
∴AE⊥OM,
∴AE是⊙O的切線;
(2)設⊙O的半徑為R,
∵OM∥BE,
∴△OMA∽△BEA,
∴![]() =
=![]() 即
即![]() =
=![]() ,
,
解得R=3,
∴⊙O的半徑為3;
(3)過點O作OH⊥BG于點H,則BG=2BH,
∵∠OME=∠MEH=∠EHO=90°,
∴四邊形OMEH是矩形,
∴HE=OM=3,
∴BH=1,
∴BG=2BH=2.


科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O直徑,直徑AB⊥弦CD于點E,四邊形ADCF是平行四邊形,CD=4![]() ,BE=2.
,BE=2.

(1)求⊙O直徑和弦AD的長;
(2)求證:FC是⊙O切線.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數y=![]() 的圖象的一支位于第一象限.
的圖象的一支位于第一象限.
(1)判斷該函數圖象的另一支所在的象限,并求m的取值范圍;
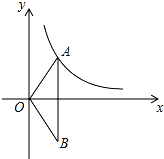
(2)如圖,O為坐標原點,點A在該反比例函數位于第一象限的圖象上,點B與點A關于x軸對稱,若△OAB的面積為10,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若∠A和∠B的兩邊分別平行,且∠A比∠B的3倍少20°,則∠B的度數為( )
A. 10° B. 70° C. 10°或50° D. 70°或50°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨州市尚市“桃花節”觀賞人數逐年增加,據有關部門統計,2014年約為20萬人次,2016年約為28.8萬人次,設觀賞人數年均增長率為x,則下列方程中正確的是( )
A.20(1+2x)=28.8
B.28.8(1+x)2=20
C.20(1+x)2=28.8
D.20+20(1+x)+20(1+x)2=28.8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,定義:在直角三角形ABC中,銳角α的鄰邊與對邊的比叫做角α的余切,記作ctanα,即ctanα=![]() =
=![]() ,根據上述角的余切定義,解下列問題:
,根據上述角的余切定義,解下列問題:
(1)如圖1,若BC=3,AB=5,則ctanB= ;
(2)ctan60°= ;
(3)如圖2,已知:△ABC中,∠B是銳角,ctan C=2,AB=10,BC=20,試求∠B的余弦cosB的值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com