
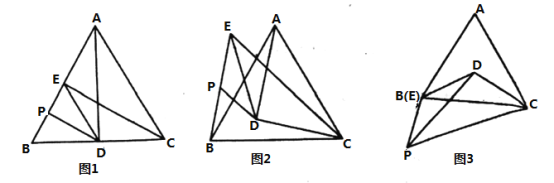
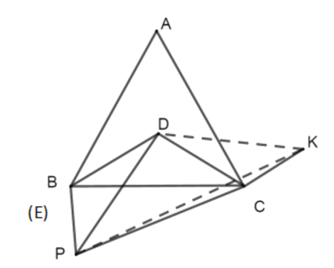
【題目】已知等邊![]() 和等腰
和等腰![]() ,
,![]() ,
,![]() .
.
(1)如圖1,點![]() 在
在![]() 上,點
上,點![]() 在
在![]() 上,
上,![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,則線段
,則線段![]() 與
與![]() 之間的數量關系為 ;
之間的數量關系為 ;
(2)如圖2,點![]() 在
在![]() 內部,點
內部,點![]() 在
在![]() 外部,
外部,![]() 是
是![]() 的中點,連接
的中點,連接![]() ,
,![]() ,則(1)中的結論是否仍然成立?若成立,請給出證明,若不成立,請說明理由.
,則(1)中的結論是否仍然成立?若成立,請給出證明,若不成立,請說明理由.
(3)如圖3,若點![]() 在
在![]() 內部,點
內部,點![]() 和點
和點![]() 重合,點
重合,點![]() 在
在![]() 下方,且
下方,且![]() 為定值,當
為定值,當![]() 最大時,
最大時,![]() 的度數為 .
的度數為 .
【答案】(1)![]()
![]() ;
;
(2)成立,理由見解析;
(3)![]()
【解析】
(1)根據等邊三角形的性質,![]() ,
,![]() ,可得
,可得![]() 是等邊三角形,
是等邊三角形,![]() 是
是![]() 的中點,利用等邊三角形三線合一性質,以及
的中點,利用等邊三角形三線合一性質,以及![]() 得出
得出![]() ,所以PD是
,所以PD是![]() 中位線,得出點D是BC的中點,AD=CE,可得出結論
中位線,得出點D是BC的中點,AD=CE,可得出結論![]()
![]() .
.
(2)作輔助線,延長ED到F,使得![]() ,使得
,使得![]() 是等邊三角形,PD是
是等邊三角形,PD是![]() 的中位線,通過證明三角形全等得出
的中位線,通過證明三角形全等得出![]() 可證明結論.
可證明結論.
(3)作出等腰![]() ,由旋轉模型證明三角形
,由旋轉模型證明三角形![]() ,利用P、C、K三點共線時,PK最大,即PD最大可求解得.
,利用P、C、K三點共線時,PK最大,即PD最大可求解得.
(1)根據圖1,在等邊![]() 和等腰
和等腰![]() 中,
中,
![]()
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 是等邊三角形,
是等邊三角形,
![]()
![]() 是
是![]() 的中點,
的中點,
![]() ,
,
![]() ,
,![]() ,
,
![]() PD是
PD是![]() 中位線
中位線
![]() 分別是
分別是![]() 的中點,
的中點,
![]() ,
,
故答案為:![]()
![]() .
.
(2)結論成立.
理由:如下圖中,延長ED到F,使得![]() ,連接FC,BF,
,連接FC,BF,
![]() ,
,
![]()
![]()
![]()
![]()
![]() 是等邊三角形,
是等邊三角形,
![]() ,
,
在![]() 和
和![]() 中
中
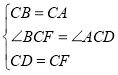
![]()
![]() ,
,
![]() ,
,
![]() ,
,
故答案為:結論成立;
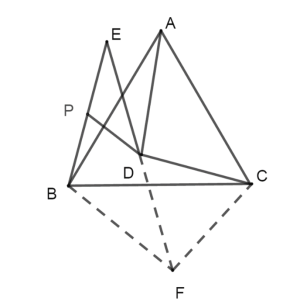
(3)作![]() ,且
,且![]() ,
,
連接PK,DK,
則![]() 為等腰三角形,
為等腰三角形,
在![]() 和
和![]() 中
中
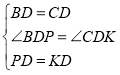
![]() ,
,
![]() ,
,
即![]() 為定值.
為定值.
P、C、K三點共線時,PK最大,即PD最大,
![]() 此時,
此時,![]() ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】已知A,B兩地相距120千米,甲乙兩人沿同一條公路勻速行駛,甲騎自行車以20千米/時從A地前往B地,同時乙騎摩托車從B地前往A地,設兩人之間的距離為s(千米),甲行駛的時間為t(小時),若s與t的函數關系如圖所示,則下列說法錯誤的是( )
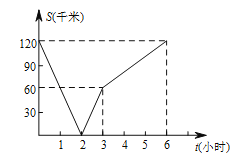
A.經過2小時兩人相遇
B.若乙行駛的路程是甲的2倍,則t=3
C.當乙到達終點時,甲離終點還有60千米
D.若兩人相距90千米,則t=0.5或t=4.5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“一帶一路”戰略的影響下,某茶葉經銷商準備把“茶路”融入“絲路”,經計算,他銷售10斤A級別和20斤B級別茶葉的利潤為4000元,銷售20斤A級別和10斤B級別茶葉的利潤為3500元
(1)分別求出每斤A級別茶葉和每斤B級別茶葉的銷售利潤;
(2)若該經銷商一次購進兩種級別的茶葉共200斤用于出口.設購買A級別茶葉a斤(70≤a≤120),銷售完A、B兩種級別茶葉后獲利w元.
①求出w與a之間的函數關系式;
②該經銷商購進A、B兩種級別茶葉各多少斤時,才能獲取最大的利潤,最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是“作圓的內接正方形”的尺規作圖過程。
已知:⊙O.
求作:圓的內接正方形.
如圖,
(1)過圓心O作直線AC,與⊙O相交于A,C兩點;
(2)過點O作直線BD⊥AC,交⊙O于B,D兩點;
(3)連接AB,BC,CD,DA。
∴四邊形ABCD為所求。

請回答:該尺規作圖的依據是____________________________。(寫出兩條)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某班數學興趣小組對不等式組![]() ,討論得到以下結論:①若a=5,則不等式組的解集為3<x≤5;②若a=2,則不等式組無解;③若不等式組無解,則a的取值范圍為a<3;④若不等式組只有兩個整數解,則a的值可以為5.1,其中,正確的結論的序號是____.
,討論得到以下結論:①若a=5,則不等式組的解集為3<x≤5;②若a=2,則不等式組無解;③若不等式組無解,則a的取值范圍為a<3;④若不等式組只有兩個整數解,則a的值可以為5.1,其中,正確的結論的序號是____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】漣水外賣市場競爭激烈,美團、餓了么等公司訂單大量增加,某公司負責招聘外賣送餐員,具體方案如下:每月不超出750單,每單收入4元;超出750單的部分每單收入m元.
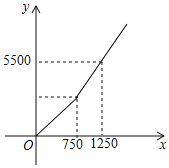
(1)若某“外賣小哥”某月送了500單,收入 元;
(2)若“外賣小哥”每月收入為y(元),每月送單量為x單,y與x之間的關系如圖所示,求y與x之間的函數關系式;
(3)若“外賣小哥”甲和乙在某個月內共送單1200單,且甲送單量低于乙送單量,共收入5000元,問:甲、乙送單量各是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△![]() 和△
和△![]() 中,
中,![]() ,
,![]() 和
和![]() 分別為
分別為![]() 邊和
邊和![]() 邊上的中線,再從以下三個條件:①
邊上的中線,再從以下三個條件:①![]() ;②
;②![]() ;③
;③![]() 中任取兩個為已知條件,另一個為結論,則最多可以構成_______個正確的命題.
中任取兩個為已知條件,另一個為結論,則最多可以構成_______個正確的命題.
查看答案和解析>>
科目:初中數學 來源: 題型:
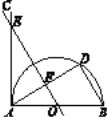
【題目】已知:如圖, ![]() 是半圓
是半圓![]() 的直徑,D是半圓上的一個動點(點D不與點A,B 重合),
的直徑,D是半圓上的一個動點(點D不與點A,B 重合), ![]()
(1)求證:AC是半圓![]() 的切線;
的切線;

(2)過點O作BD的平行線,交AC于點E,交AD于點F,且EF=4, AD=6, 求BD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現
如圖1,△ACB和△DCE均為等邊三角形,點A,D,E在同一直線上,連接BE.填空:
①∠AEB的度數為______;
②線段AD,BE之間的數量關系為______.
(2)拓展探究
如圖2,△ACB和△DCE均為等腰直角三角形,∠ACB=∠DCE=90°,點A,D,E在同一直線上,CM為△DCE中DE邊上的高,連接BE,請判斷∠AEB的度數及線段CM,AE,BE之間的數量關系,并說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com