
【題目】為更新果樹品種,某果園計劃新購進A、B兩個品種的果樹苗栽植培育,若計劃購進這兩種果樹苗共45棵,其中A種苗的單價為7元/棵,購買B種苗所需費用y(元)與購買數量x(棵)之間存在如圖所示的函數關系. 
(1)求y與x的函數關系式;
(2)若在購買計劃中,B種苗的數量不超過35棵,但不少于A種苗的數量,請設計購買方案,使總費用最低,并求出最低費用.
【答案】
(1)解:設y與x的函數關系式為:y=kx+b,
當0≤x≤20時,把(0,0),(20,160)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
此時y與x的函數關系式為y=8x;
當20≤x時,把(20,160),(40,288)代入y=kx+b中,
得: ![]() ,解得:
,解得: ![]() ,
,
此時y與x的函數關系式為y=6.4x+32.
綜上可知:y與x的函數關系式為y= 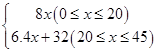
(2)解:∵B種苗的數量不超過35棵,但不少于A種苗的數量,
∴ ![]() ,
,
∴22.5≤x≤35,
設總費用為W元,則W=6.4x+32+7(45﹣x)=﹣0.6x+347,
∵k=﹣0.6,
∴y隨x的增大而減小,
∴當x=35時,W總費用最低,W最低=﹣0.6×35+347=326(元)
【解析】(1)根據函數圖象找出點的坐標,結合點的坐標分段利用待定系數法求出函數解析式即可;(2)根據B種苗的數量不超過35棵,但不少于A種苗的數量可得出關于x的一元一次不等式組,解不等式組求出x的取值范圍,再根據“所需費用為W=A種樹苗的費用+B種樹苗的費用”可得出W關于x的函數關系式,根據一次函數的性質即可解決最值問題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,直線y=﹣x+10與x軸、y軸分別交于點B,C,點A的坐標為(8,0),P(x,y)是直線y=﹣x+10在第一象限內一個動點.
(1)求△OPA的面積S與x的函數關系式,并寫出自變量的x的取值范圍;
(2)當△OPA的面積為10時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】請觀察下列算式,找出規律并填空
①![]() =1﹣
=1﹣![]() ,②
,②![]() =
=![]() ×(1﹣
×(1﹣![]() ),③
),③![]() =
=![]() ×(1﹣
×(1﹣![]() ),④
),④![]() =
=![]() ×(1﹣
×(1﹣![]() ),…
),…
(1)則第10個算式是______,
(2)第n個算式為_______=_______.
(3)從以上規律中你可得到一些啟示嗎?根據你得到的啟示,試解答下題:
若有理數a、b滿足|a﹣1|+(b﹣3)2=0,
求![]() +
+![]() +
+![]() +…+
+…+![]() 的值.
的值.
(4)如圖,把一個面積為1的正方形等分成兩個面積為![]() 的長方形,接著把面積為
的長方形,接著把面積為![]() 的長方形等分成兩個面積為
的長方形等分成兩個面積為![]() 的正方形,再把面積為
的正方形,再把面積為![]() 的正方形等分成兩個面積為
的正方形等分成兩個面積為![]() 的矩形.如此進行下去,試利用圖形揭示的規律計算:
的矩形.如此進行下去,試利用圖形揭示的規律計算:![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() (直接寫答案)
(直接寫答案)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,∠1=∠2,則不一定能使△ABD≌△ACD的條件是 ( )
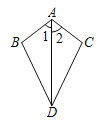
A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方形OABC中,O為平面直角坐標系的原點,A點的坐標為![]() ,C點的坐標為
,C點的坐標為![]() ,點B在第一象限內,點P從原點出發,以每秒2個單位長度的速度沿著
,點B在第一象限內,點P從原點出發,以每秒2個單位長度的速度沿著![]() 的路線移動
的路線移動![]() 即:沿著長方形移動一周
即:沿著長方形移動一周![]() .
.
![]() 寫出點B的坐標
寫出點B的坐標![]() ______
______![]()
![]() 當點P移動了4秒時,描出此時P點的位置,并求出點P的坐標.
當點P移動了4秒時,描出此時P點的位置,并求出點P的坐標.
![]() 在移動過程中,當點P到x軸距離為5個單位長度時,求點P移動的時間.
在移動過程中,當點P到x軸距離為5個單位長度時,求點P移動的時間.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,BC>AD,∠B與∠C互余, 將AB,CD分別平移到EF和EG的位置,則△EFG為________三角形,若AD=2cm,BC=8cm,則FG=____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,∠BAC=1200,以BC為邊向形外作等邊三角形△BCD,把△ABD繞著點D按順時針方向旋轉600后得到△ECD,若AB=3,AC=2,求∠BAD的度數與AD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
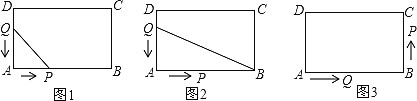
【題目】如圖,在長方形ABCD中,AB=12厘米,BC=6厘米.點P沿AB邊從點A開始向點B以2cm/s的速度移動;點Q沿DA邊從點D開始向點A以1cm、s的速度移動.如果P、Q同時出發,用![]() (秒)表示移動的時間,那么:
(秒)表示移動的時間,那么:
(1)如圖1,當![]() 為何值時,△QAP為等腰直角三角形?
為何值時,△QAP為等腰直角三角形?
(2)如圖2,當![]() 為何值時,△QAB的面積等于長方形面積的
為何值時,△QAB的面積等于長方形面積的![]()
(3)如圖3,P、Q到達B、A后繼續運動,P點到達C點后都停止運動.當![]() 為何值時,線段AQ的長等于線段CP的長的一半?
為何值時,線段AQ的長等于線段CP的長的一半?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學老師布置了一道思考題,“計算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )”,小明仔細思考了一番,用了一種不同的方法解決了這個問題.
)”,小明仔細思考了一番,用了一種不同的方法解決了這個問題.
小明的解法:原式的倒數為(![]() ﹣
﹣![]() )÷(﹣
)÷(﹣![]() )…第一步
)…第一步
=(![]() ﹣
﹣![]() )×(﹣12)…第二步
)×(﹣12)…第二步
=﹣4+10…第三步
=6…第四步
所以(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() )=
)=![]() .
.
(1)小明解法第二步到第三步的運算依據是什么?
(2)請你運用小明的解法計算:(﹣![]() )÷(
)÷(![]() ﹣
﹣![]() +
+![]() ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com