
【題目】為豐富學生課余生活,我校準備開設興趣課堂.為了了解學生對繪畫、書法、舞蹈、樂器這四個興趣小組的喜愛情況,在全校進行隨機抽樣調查,并根據收集的數據繪制了下面兩幅統計圖(信息尚不完整),請根據圖中提供的信息,解答下面的問題:

(1)此次共調查了多少名同學?
(2)將條形圖補充完整,并計算扇形統計圖中樂器部分的圓心角的度數;
(3)如果我校共有1000名學生參加這4個課外興趣小組,而每個教師最多只能輔導本組的25名學生,估計書法興趣小組至少需要準備多少名教師?
【答案】(1)200;(2)圖詳見解析,108°;(3)4.
【解析】
(1)根據參加繪畫小組的人數是90,所占的百分比是45%,即可求得調查的總人數;
(2)利用360°乘以對應的比例即可求得圓心角的度數;
(3)利用樣本估計總體的方法求出各書法興趣小組的人數,再除以25即可解答.
(1)共有學生:90÷45%=200(人),
答:此次共調查了200名同學;
(2)喜愛樂器小組的人數是200-90-20-30=60(人);
扇形統計圖中樂器部分的圓心角的度數是360°×![]() =108°.
=108°.

(3)學習書法有![]() ×1000=100(人),
×1000=100(人),
需要書法教師:100÷25=4(人),
答:估計書法興趣小組至少需要準備4名教師.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】已知A=﹣xy+x+1,B=4x+3y,
(1)當x=﹣2, y=0.6時,求A+2B的值;
(2)若代數式2A﹣B的結果與字母y的取值無關,求x的值
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】張師傅在鋪瓷磚時發現,用8塊大小一樣的小長方形瓷磚恰好可以拼成一個大的長方形,如圖①.然后,他用這8塊瓷磚又拼出一個正方形,如圖②,中間恰好空出一個邊長為1的小正方形(陰影部分).
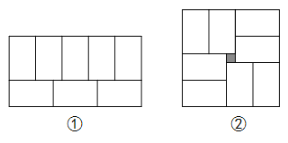
(1)請你根據圖①寫出小長方形的長與寬之比為 ;
(2)請你根據圖②列出方程,求出小長方形的長與寬.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】宇航員翟志剛在太空進行了19分35秒的艙外活動中,飛行了9 165 000 米,成為中國“飛得最高、走得最快”的人.將9 165 000 米保留兩位有效數字用科學記數法記為( )米
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠C=90°,以AC為直徑作⊙O,交AB于D,過點O作OE∥AB,交BC于E.
(1)求證:ED為⊙O的切線;
(2)如果⊙O的半徑為![]() ,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.
,ED=2,延長EO交⊙O于F,連接DF、AF,求△ADF的面積.

【答案】(1)證明見解析;(2)![]()
【解析】試題分析:(1)首先連接OD,由OE∥AB,根據平行線與等腰三角形的性質,易證得![]() ≌
≌![]() 即可得
即可得![]() ,則可證得
,則可證得![]() 為
為![]() 的切線;
的切線;
(2)連接CD,根據直徑所對的圓周角是直角,即可得![]() 利用勾股定理即可求得
利用勾股定理即可求得![]() 的長,又由OE∥AB,證得
的長,又由OE∥AB,證得![]() 根據相似三角形的對應邊成比例,即可求得
根據相似三角形的對應邊成比例,即可求得![]() 的長,然后利用三角函數的知識,求得
的長,然后利用三角函數的知識,求得![]() 與
與![]() 的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
的長,然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案.
試題解析:(1)證明:連接OD,

∵OE∥AB,
∴∠COE=∠CAD,∠EOD=∠ODA,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠COE=∠DOE,
在△COE和△DOE中,
 ∴△COE≌△DOE(SAS),
∴△COE≌△DOE(SAS),
![]()
∴ED⊥OD,
∴ED是![]() 的切線;
的切線;
(2)連接CD,交OE于M,
在Rt△ODE中,
∵OD=32,DE=2,
![]()
∵OE∥AB,
∴△COE∽△CAB,
![]() ∴AB=5,
∴AB=5,
∵AC是直徑,
![]()
![]()
![]()
![]()
∵EF∥AB,
![]()
![]()
![]()
∴S△ADF=S梯形ABEFS梯形DBEF
![]()
∴△ADF的面積為![]()

【題型】解答題
【結束】
25
【題目】【題目】已知,拋物線y=ax2+ax+b(a≠0)與直線y=2x+m有一個公共點M(1,0),且a<b.
(1)求b與a的關系式和拋物線的頂點D坐標(用a的代數式表示);
(2)直線與拋物線的另外一個交點記為N,求△DMN的面積與a的關系式;
(3)a=﹣1時,直線y=﹣2x與拋物線在第二象限交于點G,點G、H關于原點對稱,現將線段GH沿y軸向上平移t個單位(t>0),若線段GH與拋物線有兩個不同的公共點,試求t的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將6張小長方形紙片(如圖1所示)按圖2所示的方式不重疊的放在長方形ABCD內,未被覆蓋的部分恰好分割為兩個長方形,面積分別為S1和S2.已知小長方形紙片的長為a,寬為b,且a>b.當AB長度不變而BC變長時,將6張小長方形紙片還按照同樣的方式放在新的長方形ABCD內,S1與S2的差總保持不變,則a,b滿足的關系是

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,一次函數y=kx+3的圖象與反比例函數y=![]() (x>0)的圖象交于點P.PA⊥x軸于點A,PB⊥y軸于點B. 一次函數的圖象分別交x軸、y軸于點C. 點D,且S△DBP=27,
(x>0)的圖象交于點P.PA⊥x軸于點A,PB⊥y軸于點B. 一次函數的圖象分別交x軸、y軸于點C. 點D,且S△DBP=27,![]()
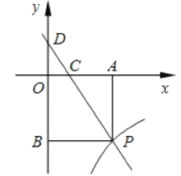
(1)求點D的坐標;
(2)求一次函數與反比例函數的解析式
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,是假命題的是( )
A. 過![]() 邊形一個頂點的所有對角線,將這個多邊形分成
邊形一個頂點的所有對角線,將這個多邊形分成![]() 個三角形
個三角形
B. 三角形中,到三個頂點距離相等的點是三條邊垂直平分線的交點
C. 三角形的中線將三角形分成面積相等的兩部分
D. 一組對邊平行另一組對邊相等的四邊形是平行四邊形
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某村耕地總面積為50公頃,且該村人均耕地面積y(單位:公頃/人)與總人口x(單位:人)的函數圖象如圖所示,則下列說法正確的是( )
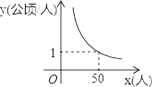
A. 該村人均耕地面積隨總人口的增多而增多
B. 該村人均耕地面積y與總人口x成正比例
C. 若該村人均耕地面積為2公頃,則總人口有100人
D. 當該村總人口為50人時,人均耕地面積為1公頃
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com