
【題目】在平面直角坐標系xOy中,已知點A(0,3m),P(0,2m),Q(0,m)(m≠0).將點A繞點P順時針旋轉90°,得到點M,將點O繞點Q順時針旋轉90°,得到點N,連接MN,稱線段MN為線段AO的伴隨線段.
(1)如圖1,若m=1,則點M,N的坐標分別為 , ;
(2)對于任意的m,求點M,N的坐標(用含m的式子表示);
(3)已知點B(![]() ,t),C(
,t),C(![]() ,t),以線段BC為直徑,在直線BC的上方作半圓,若半圓與線段BC圍成的區(qū)域內(nèi)(包括邊界)至少存在一條線段AO的伴隨線段MN,直接寫出t的取值范圍.
,t),以線段BC為直徑,在直線BC的上方作半圓,若半圓與線段BC圍成的區(qū)域內(nèi)(包括邊界)至少存在一條線段AO的伴隨線段MN,直接寫出t的取值范圍.
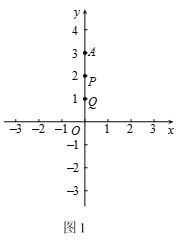

【答案】(1)(1,2),(1,1) .(2)(m,2 m),(m, m).(3)![]() .
.
【解析】
(1)把m=1分別代入點A,P,Q的坐標中,依據(jù)題意進行操作即可得到M,N的坐標;
(2)根據(jù)點A,P,Q的坐標求出AP,OP,OQ的長,再根據(jù)旋轉的性質(zhì)可求出M,N的坐標;
(3)分m為正數(shù)和負數(shù)兩種情況討論求解即可.
(1)∵A(0,3m),P(0,2m),Q(0,m)
∴當m=1時,A(0,3),P(0,2),Q(0,1)
∵點A繞點P順時針旋轉90°,得到點M,
∴M(1,2)
∵點O繞點Q順時針旋轉90°,得到點N,
∴N(-1,1),如圖所示:
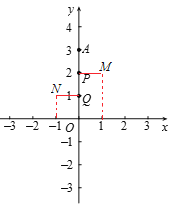
(2)∵A(0,3m),P(0,2m),Q(0,m)
∴AP=m,OP=2m,OQ=m
∵點A繞點P順時針旋轉90°,得到點M,
∴M(m,2m)
∵點O繞點Q順時針旋轉90°,得到點N,
∴N(-m,m);
(3)∵點B(![]() ,t),C(
,t),C(![]() ,t),
,t),
∴BC=2![]()
以線段BC為直徑,在直線BC的上方作半圓,如圖所示,
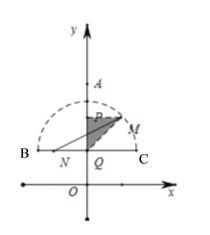
①當m為正數(shù)時,半圓中線段MN的最大值是N在BC上,M在弧上,
此時△PQM是等腰直角三角形,
∴![]() ,即
,即![]()
解得m=1或m=-1(舍去),
∴QO=1,
∴t=1;
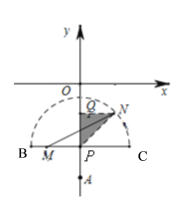
②當m為負數(shù)時,半圓中線段MN的最小值是M在BC上,N在弧上,此時△PQM是等腰直角三角形,如圖,
∴![]() ,即
,即![]()
解得m=-1或m=1(舍去),
∴PO=2,
∴t=-2;
故![]()


科目:初中數(shù)學 來源: 題型:
【題目】參照學習函數(shù)的過程與方法,探究函數(shù)y=![]() 的圖象與性質(zhì).
的圖象與性質(zhì).
因為y=![]() ,即y=﹣
,即y=﹣![]() +1,所以我們對比函數(shù)y=﹣
+1,所以我們對比函數(shù)y=﹣![]() 來探究.
來探究.
列表:
x | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | ﹣ |
| 1 | 2 | 3 | 4 | … |
y=﹣ | … |
|
| 1 | 2 | 4 | ﹣4 | ﹣1 | 1 | ﹣ | ﹣ | … |
y= | … |
|
| 2 | 3 | 5 | ﹣3 | ﹣1 | 0 |
|
| … |
描點:在平面直角坐標系中,以自變量x的取值為橫坐標,以y=![]() 相應的函數(shù)值為縱坐標,描出相應的點,如圖所示:
相應的函數(shù)值為縱坐標,描出相應的點,如圖所示:
(1)請把y軸左邊各點和右邊各點,分別用一條光滑曲線順次連接起來;
(2)觀察圖象并分析表格,回答下列問題:
①當x<0時,y隨x的增大而 ;(填“增大”或“減小”)
②y=![]() 的圖象是由y=﹣
的圖象是由y=﹣![]() 的圖象向 平移 個單位而得到;
的圖象向 平移 個單位而得到;
③圖象關于點 中心對稱.(填點的坐標)
(3)設A(x1,y1),B(x2,y2)是函數(shù)y=![]() 的圖象上的兩點,且x1+x2=0,試求y1+y2+3的值.
的圖象上的兩點,且x1+x2=0,試求y1+y2+3的值.
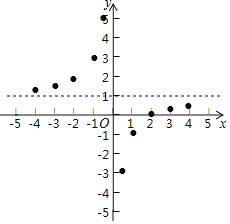
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】彈簧是一種利用彈性來工作的機械零件,用彈性材料制成的零件在外力作用下發(fā)生形變,除去外力后又恢復原狀.某班同學在探究彈簧的長度與所受外力的變化關系時,通過實驗記錄得到的數(shù)據(jù)如下表:
砝碼的質(zhì)量x(克) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 | 500 |
指針的位置y(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 | 7.5 |
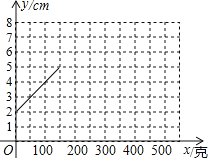
小騰根據(jù)學習函數(shù)的經(jīng)驗,利用上述表格所反映出的y與x之間的變化規(guī)律,對該函數(shù)的圖象與性質(zhì)進行了探究,下面是小騰的探究過程,請補充完整.
(1)根據(jù)上述表格在平面直角坐標系中補全該函數(shù)的圖象;
(2)根據(jù)畫出的函數(shù)圖象,寫出:
①當x=0時,y= ,它的實際意義是 ;
②當指針的位置y不變時,砝碼的質(zhì)量x的取值范圍為 .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】如圖,點O為Rt△ABC斜邊AB上的一點,以OA為半徑的⊙O與邊BC交于點D,與邊AC交于點E,連接AD,且AD平分∠BAC.
(1)試判斷BC與⊙O的位置關系,并說明理由;
(2)若∠BAC=60°,OA=2,求陰影部分的面積(結果保留π).

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】某中學數(shù)學興趣小組在一次課外學習與探究中遇到一些新的數(shù)學符號,他們將其中某些材料摘錄如下:
對于三個實,數(shù)![]() ,
,![]() ,
,![]() ,用
,用![]() 表示這三個數(shù)的平均數(shù),用
表示這三個數(shù)的平均數(shù),用![]() 表示這三個數(shù)中最小的數(shù),例如
表示這三個數(shù)中最小的數(shù),例如![]()
![]() =4,
=4,![]() ,
,![]() .請結合上述材料,解決下列問題:
.請結合上述材料,解決下列問題:
(1)①![]() _____,
_____,
②![]() _____;
_____;
(2)若![]() ,則
,則![]() 的取值范圍為_____;
的取值范圍為_____;
(3)若![]() ,求
,求![]() 的值;
的值;
(4)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】已知關于![]() 的二次函數(shù)
的二次函數(shù)![]() 的圖象開口向下,
的圖象開口向下,![]() 與
與![]() 的部分對應值如下表所示:
的部分對應值如下表所示:
|
|
|
|
|
|
|
|
|
|
|
|
下列判斷,①![]() ;②
;②![]() ;③方程
;③方程![]() 有兩個不相等的實數(shù)根;
有兩個不相等的實數(shù)根;
④若![]() ,則
,則![]() ,正確的是________________(填寫正確答案的序號) .
,正確的是________________(填寫正確答案的序號) .
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
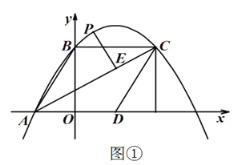
【題目】如圖①,直線![]() 與
與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() 兩點,將
兩點,將![]() 沿
沿![]() 軸正方向平移后,點
軸正方向平移后,點![]() 、點
、點![]() 的對應點分別為點
的對應點分別為點![]() 、點
、點![]() ,且四邊形
,且四邊形![]() 為菱形,連接
為菱形,連接![]() ,拋物線
,拋物線![]() 經(jīng)過
經(jīng)過![]() 三點,點
三點,點![]() 為
為![]() 上方拋物線上一動點,作
上方拋物線上一動點,作![]() ,垂足為
,垂足為![]()
![]() 求此拋物線的函數(shù)關系式;
求此拋物線的函數(shù)關系式;
![]() 求線段
求線段![]() 長度的最大值;
長度的最大值;
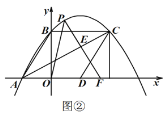
![]() 如圖②,延長
如圖②,延長![]() 交
交![]() 軸于點
軸于點![]() ,連接
,連接![]() ,若
,若![]() 為等腰三角形,請直接寫出點
為等腰三角形,請直接寫出點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
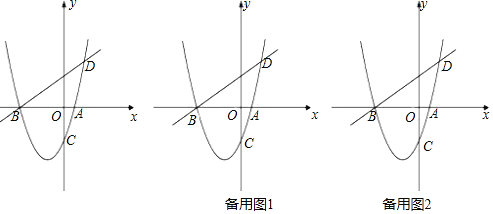
【題目】如圖,已知拋物線![]() 與x軸交于A、B兩點,與y軸交于C點,直線BD交拋物線于點D,并且
與x軸交于A、B兩點,與y軸交于C點,直線BD交拋物線于點D,并且![]() ,
,![]() .
.
(1)求拋物線的解析式;
(2)已知點M為拋物線上一動點,且在第三象限,順次連接點B、M、C,求![]() 面積的最大值;
面積的最大值;
(3)在(2)中![]() 面積最大的條件下,過點M作直線平行于y軸,在這條直線上是否存在一個以Q點為圓心,OQ為半徑且與直線AC相切的圓?若存在,求出圓心Q的坐標;若不存在,請說明理由.
面積最大的條件下,過點M作直線平行于y軸,在這條直線上是否存在一個以Q點為圓心,OQ為半徑且與直線AC相切的圓?若存在,求出圓心Q的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=mx2﹣6mx+9m+1(m≠0).
(1)求拋物線的頂點坐標;
(2)若拋物線與x軸的兩個交點分別為A和B點(點A在點B的左側),且AB=4,求m的值.
(3)已知四個點C(2,2)、D(2,0)、E(5,﹣2)、F(5,6),若拋物線與線段CD和線段EF都沒有公共點,請直接寫出m的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com