
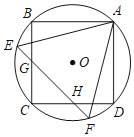
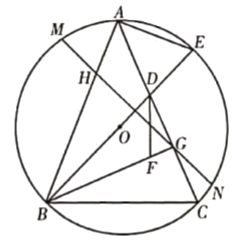
【題目】如圖,正方形ABCD和等邊△AEF都內接于圓O,EF與BC、CD別相交于點G、H.若AE=6,則EG的長為( )
A.![]() B.3﹣
B.3﹣![]() C.
C.![]() D.2
D.2![]() ﹣3
﹣3
【答案】B
【解析】
連接AC、BD、OF,AC與EF交于P點,則它們的交點為O點,如圖,利用正方形和等邊三角形的性質得到∠COF=60°,AC⊥BD,∠BCA=45°,利用含30度的直角三角形三邊的關系得到OP=![]() OF=
OF=![]() OC,OP=
OC,OP=![]() PF=
PF=![]() ,從而得到PC=OP=
,從而得到PC=OP=![]() ,然后利用△PCG為等腰直角三角形得到PG=PC=
,然后利用△PCG為等腰直角三角形得到PG=PC=![]() ,從而得到EG的長.
,從而得到EG的長.
連接AC、BD、OF,AC與EF交于P點,則它們的交點為O點,如圖,
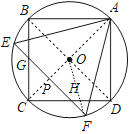
∵正方形ABCD和等邊△AEF都內接于圓O,
∴正方形ABCD和等邊△AEF都是軸對稱圖形,直徑AC是對稱軸,
∴∠COF=60°,AC⊥BD,AC⊥EF,∠BCA=45°,
∴PE=PF=![]() EF=3,
EF=3,
在Rt△OPF中,OP=![]() OF=
OF=![]() OC,
OC,
∵OP=![]() PF=
PF=![]() ,
,
∴PC=OP=![]() ,
,
∵△PCG為等腰直角三角形,
∴PG=PC=![]() ,
,
∴EG=PE﹣PG=3﹣![]() .
.
故選:B.


科目:初中數學 來源: 題型:
【題目】正方形![]() 的邊長為3,點
的邊長為3,點![]() ,
,![]() 分別在射線
分別在射線![]() ,
,![]() 上運動,且
上運動,且![]() .連接
.連接![]() ,作
,作![]() 所在直線于點
所在直線于點![]() ,連接
,連接![]() .
.
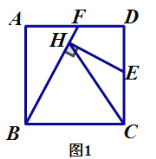

(1)如圖1,若點![]() 是
是![]() 的中點,
的中點,![]() 與
與![]() 之間的數量關系是______;
之間的數量關系是______;
(2)如圖2,當點![]() 在
在![]() 邊上且不是
邊上且不是![]() 的中點時,(1)中的結論是否成立?若成立給出證明;若不成立,說明理由;
的中點時,(1)中的結論是否成立?若成立給出證明;若不成立,說明理由;
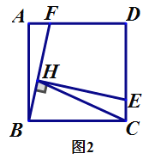
(3)如圖3,當點![]() ,
,![]() 分別在射線
分別在射線![]() ,
,![]() 上運動時,連接
上運動時,連接![]() ,過點
,過點![]() 作直線
作直線![]() 的垂線,交直線
的垂線,交直線![]() 于點
于點![]() ,連接
,連接![]() ,求線段
,求線段![]() 長的最大值.
長的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩位運動員在相同條件下各射擊![]() 次,成績如下: 甲:
次,成績如下: 甲:![]() ; 乙:
; 乙:![]() 根據上述信息,下列結論錯誤的是( )
根據上述信息,下列結論錯誤的是( )
A.甲、乙的眾數分別是![]() B.甲、乙的中位數分別是
B.甲、乙的中位數分別是![]()
C.乙的成績比較穩定D.甲、乙的平均數分別是![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了預測本校九年級男生畢業體育測試達標情況,隨機抽取該年級部分男生進行了一次測試(滿分50分,成績均記為整數分),并按測試成績![]() (單位:分)分成四類:
(單位:分)分成四類:![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() ),
),![]() 類(
類(![]() )繪制出如圖所示的不完整條形統計圖,請根據圖中信息解答下列問題:
)繪制出如圖所示的不完整條形統計圖,請根據圖中信息解答下列問題:
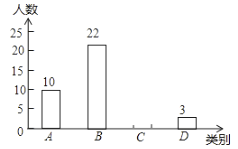
成績等級 | 人數 | 所占百分比 |
| 10 |
|
| 22 |
|
|
|
|
| 3 |
|
(1)![]() ______,
______,![]() _______,
_______,![]() _________;
_________;
(2)補全條形統計圖;
(3)若該校九年級男生有600名,![]() 類為測試成績不達標,請估計該校九年級男生畢業體育測試成績能達標的有多少名?
類為測試成績不達標,請估計該校九年級男生畢業體育測試成績能達標的有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
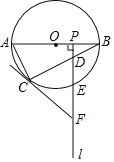
【題目】如圖,![]() 是
是![]() 的直徑,點
的直徑,點![]() 為
為![]() 上一點,點
上一點,點![]() 是半徑
是半徑![]() 上一動點(不與
上一動點(不與![]() ,
,![]() 重合),過點
重合),過點![]() 作射線
作射線![]() ,分別交弦
,分別交弦![]() ,
,![]() 于
于![]() ,
,![]() 兩點,在射線
兩點,在射線![]() 上取點
上取點![]() ,使
,使![]() .
.
(1)求證:![]() 是
是![]() 的切線;
的切線;
(2)當點![]() 是
是![]() 的中點時,
的中點時,
①若![]() ,判斷以
,判斷以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形是什么特殊四邊形,并說明理由;
為頂點的四邊形是什么特殊四邊形,并說明理由;
②若![]() ,且
,且![]() ,求
,求![]() 的長.
的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
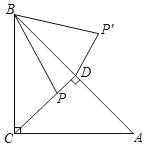
【題目】如圖,在△ABC中,∠ACB=90°,AC=BC=4,P是△ABC的高CD上一個動點,以B點為旋轉中心把線段BP逆時針旋轉45°得到BP′,連接DP′,則DP′的最小值是( )
A.2![]() -2B.4﹣2
-2B.4﹣2![]() C.2﹣
C.2﹣![]() D.
D.![]() -1
-1
查看答案和解析>>
科目:初中數學 來源: 題型:
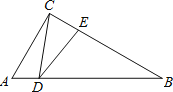
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB邊上一個動點(不與點A、B重合),E是BC邊上一點,且∠CDE=30°.設AD=x,BE=y,則下列圖象中,能表示y與x的函數關系的圖象大致是( )
A.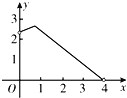 B.
B.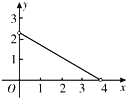 C.
C.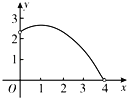 D.
D.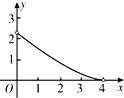
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知: ![]() 是
是![]() 的兩條弦,
的兩條弦,![]() 于點
于點![]() ,
,![]() 的平分線交
的平分線交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ,連接
,連接![]()
![]() 如圖1,求
如圖1,求![]() 的度數;
的度數;

![]() 如圖2,
如圖2,![]() 為
為![]() 上一點,連接
上一點,連接![]() ,當
,當![]() 時,求證:
時,求證:![]()

![]() 如圖3 ,在
如圖3 ,在![]() 的條件下,當
的條件下,當![]() 為
為![]() 的直徑時,經過點
的直徑時,經過點![]() 的弦
的弦![]() 交
交![]() 于點
于點![]() ,若
,若![]() 的面積為
的面積為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com