
【題目】為了更好改善河流的水質,治污公司決定購買10臺污水處理設備![]() 現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
現有A,B兩種型號的設備,其中每臺的價格,月處理污水量如下表:經調查:購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元.
A型 | B型 | |
價格 | a | b |
處理污水量 | 240 | 200 |
![]() 求a,b的值;
求a,b的值;
![]() 治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
治污公司經預算購買污水處理設備的資金不超過105萬元,你認為該公司有哪幾種購買方案;
![]() 在
在![]() 的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
的條件下,若每月要求處理污水量不低于2040噸,為了節約資金,請你為治污公司設計一種最省錢的購買方案.
【答案】(1)依題意得:![]()
解之得:![]()
(2)設購買A型設備x臺,購買B型設備(10-x)臺,
依題意得:12x+10(10-x)≤105
x≤2.5
所以該公司共有三種購買方案:
方案一,A型設備0臺,B型設備10臺
方案二,A型設備1臺,B型設備9臺
方案三,A型設備2臺,B型設備8臺
(3)在(2)問條件下,若要每月處理污水量不低于2040噸,則:
240x+200(10-x)≥2040
x≥1
所以x取1或2
若x=1,則需資金1×12+9×10=102萬
若x=2,則需資金2×12+8×10=104萬
因此為了節約資金,應選擇方案二,即A型設備1臺,B型設備9臺。
【解析】
(1)因為購買一臺A型設備比購買一臺B型設備多2萬元,購買2臺A型設備比購買3臺B型設備少6萬元,所以有![]() ,解之即可;
,解之即可;
(2)可設購買污水處理設備A型設備x臺,B型設備(10-x)臺,則有12x+10(10-x)≤105,解之確定x的值,即可確定方案;
(3)因為每月要求處理洋瀾湖的污水量不低于2040噸,所以有240x+180(10-x)≥2040,解之即可由x的值確定方案,然后進行比較,作出選擇.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知線段AB=2,MN⊥AB于點M,且AM=BM,P是射線MN上一動點,E,D分別是PA,PB的中點,過點A,M,D的圓與BP的另一交點C(點C在線段BD上),連結AC,DE.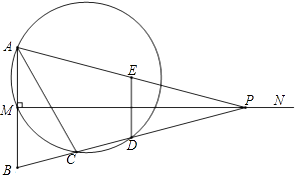
(1)當∠APB=28°時,求∠B和 ![]() 的度數;
的度數;
(2)求證:AC=AB.
(3)在點P的運動過程中
①當MP=4時,取四邊形ACDE一邊的兩端點和線段MP上一點Q,若以這三點為頂點的三角形是直角三角形,且Q為銳角頂點,求所有滿足條件的MQ的值;
②記AP與圓的另一個交點為F,將點F繞點D旋轉90°得到點G,當點G恰好落在MN上時,連結AG,CG,DG,EG,直接寫出△ACG和△DEG的面積之比.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1),AB=4cm,AC⊥AB,BD⊥AB,AC=BD=3cm.點P在線段AB上以1cm/s的速度由點A向點B運動,同時,點Q在線段BD上由點B向點D運動.它們運動的時間為t(s).
(1)若點Q的運動速度與點P的運動速度相等,當t=1時,△ACP與△BPQ是否全等,請說明理由,并判斷此時線段PC和線段PQ的位置關系;
(2)如圖(2),將圖(1)中的“AC⊥AB,BD⊥AB”為改“∠CAB=∠DBA=60°”,其他條件不變.設點Q的運動速度為x cm/s,是否存在實數x,使得△ACP與△BPQ全等?若存在,求出相應的x、t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知拋物線y= ![]() x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.
x2+bx+c與x軸交于A(﹣1,0),B(2,0)兩點,與y軸交于點C.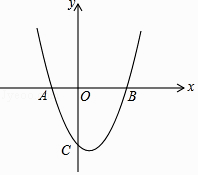
(1)求該拋物線的解析式;
(2)直線y=﹣x+n與該拋物線在第四象限內交于點D,與線段BC交于點E,與x軸交于點F,且BE=4EC.
①求n的值;
②連接AC,CD,線段AC與線段DF交于點G,△AGF與△CGD是否全等?請說明理由;
(3)直線y=m(m>0)與該拋物線的交點為M,N(點M在點N的左側),點 M關于y軸的對稱點為點M',點H的坐標為(1,0).若四邊形OM'NH的面積為 ![]() .求點H到OM'的距離d的值.
.求點H到OM'的距離d的值.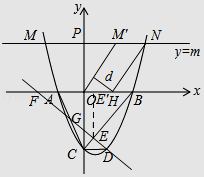
查看答案和解析>>
科目:初中數學 來源: 題型:
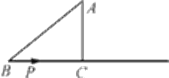
【題目】如圖,在Rt△ABC中,∠C=90°,AB=5cm,AC=3cm,動點P從點B出發沿射線BC以1cm/s的速度移動,設運動的時間為ts.
(1)求BC邊的長;
(2)當△ABP為直角三角形時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】嘉嘉在電腦上設計了一個有理數的運算程序:輸入a,加*鍵,再輸入b,得到運算a*b=(a2-b2)÷(a-b) .
(1)求(-2)*![]() *
* ![]() 的值;
的值;
(2)琪琪在運用此程序計算時,屏幕上顯示“該程序無法操作”,請你運用所學的數學知識猜想一下,琪琪在輸入數據時,可能出現什么情況?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了從甲、乙兩名選手中選拔一人參加射擊比賽,現對他們進行一次測驗,兩個人在相同條件下各射靶10次,為了比較兩人的成績,制作了如下統計圖表:
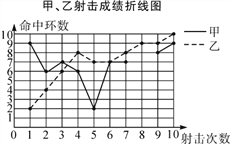
甲、乙射擊成績統計表
平均數 | 中位數 | 方差 | 命中10環的次數 | |
甲 | 7 | |||
乙 | 1 |
(1)請補全上述圖表(請直接在表中填空和補全折線圖);
(2)如果規定成績較穩定者勝出,你認為誰將勝出?說明你的理由;
(3)如果希望(2)中的另一名選手勝出,根據圖表中的信息,應該制定怎樣的評判規則?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
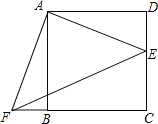
【題目】如圖,點E是正方形ABCD的邊DC上一點,把△ADE順時針旋轉△ABF的位置.
(1)旋轉中心是點 ,旋轉角度是 度;
(2)若連結EF,則△AEF是 三角形;并證明;
(3)若四邊形AECF的面積為25,DE=2,求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com