【題目】如圖，∠BAC＝∠ACD＝90°，∠ABC＝∠ADC，CE⊥AD，且BE平分∠ABC，則下列結論：①AD＝BC；②∠ACE＝∠ABC；③∠ECD＋∠EBC＝∠BEC；④∠CEF＝∠CFE．其中正的是（ ）
A. ①②B. ①③④C. ①②④D. ①②③④
【答案】D
【解析】
根據條件∠BAC＝∠ACD＝90°，∠ABC＝∠ADC可以判斷四邊形ABCD是平行四邊形，于是可判斷答案①②④正確，由④再進一步判斷答案③也正確，即可做出選擇．
解：∵∠BAC＝∠ACD＝90°，且∠ABC＝∠ADC
∴AB∥CD且∠ACB＝∠CAD
∴BC∥AD
∴四邊形ABCD是平行四邊形．
∴答案①正確；
∵∠ACE＋∠ECD＝∠D＋∠ECD＝90°
∴∠ACE＝∠D
而∠D＝∠ABC
∴∠ACE＝∠D＝∠ABC
∴答案②正確；
又∵∠CEF＋∠CBF＝90°，∠AFB＋∠ABF＝90°
且∠ABF＝∠CBF，∠AFB＝∠CFE
∴∠CEF＝∠AFB＝∠CFE
∴答案④正確；
∵∠ECD＝∠CAD，∠EBC＝∠EBA
∴∠ECD＋∠EBC＝∠CFE＝∠BEC
∴答案③正確．
故選：D．
科目：初中數學 來源： 題型：
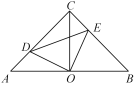
【題目】如圖，在△ABC中，∠ACB＝90°，AC＝BC，O是AB的中點，點D在AC上，點E在BC上，且∠DOE＝90°.則下列結論：①OA＝OB＝OC；②CD＝BE；③△ODE是等腰直角三角形；④四邊形CDOE的面積等于△ABC的面積的一半.其中正確的有____(填序號).
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知：在直角梯形ABCD中，AD∥BC，∠C＝90°，AB＝AD＝25，BC＝32，連接BD，AE⊥BD，垂足為E.
(1)求證：△ABE∽△DBC；
(2)求線段AE的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，P為平行四邊形ABCD邊AD上一點，E、F分別為PB、PC的中點，△PEF、△PDC、△PAB的面積分別為S、S1、S2，若S=2，則S1+S2=（ ）
A. 4 B. 6 C. 8 D. 不能確定
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀下列材料解決問題：
材料：古希臘著名數學家 畢達哥拉斯發現把數1，3，6，10，15，21…這些數量的（石子），都可以排成三角形，則稱像這樣的數為三角形數．
把數 1，3，6，10，15，21…換一種方式排列，即
1=1
1+2=3
1+2+3=6
1+2+3+4=10
1+2+3+4+5=15
…
從上面的排列方式看，把1，3，6，10，15，…叫做三角形數“名副其實”．
（1）設第一個三角形數為a1=1，第二個三角形數為a2=3，第三個三角形數為a3=6，請直接寫出第n個三角形數為an的表達式（其中n為正整數）．
（2）根據（1）的結論判斷66是三角形數嗎？若是請說出66是第幾個三角形數？若不是請說明理由．
（3）根據（1）的結論判斷所有三角形數的倒數之和T與2的大小關系并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，五邊形ABCDE中有一正三角形ACD，若AB=DE，BC=AE，∠E=115°，則∠BAE的度數為何？（ ）
A. 115 B. 120 C. 125 D. 130
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】兩個大小不同的等腰直角三角形三角板如圖1所示放置，圖2是由它抽象出的幾何圖形，B，C，E在同一條直線上，連結DC．
（1）請猜想：DC與BE的數量關系，并給予證明；
（2）求證：DC⊥BE．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在平面直角坐標系中，已知線段
，點
的坐標為
，點
的坐標為
，如圖1所示.
(1)平移線段到線段
，使點的對應點為，點的對應點為，若點的坐標為
，求點的坐標；
(2)平移線段到線段，使點在
軸的正半軸上，點在第二象限內(與對應， 與對應)，連接
如圖2所示.若
表示△BCD的面積)，求點、的坐標；
(3)在(2)的條件下，在軸上是否存在一點
，使
表示△PCD的面積)？若存在，求出點的坐標； 若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在菱形ABCD中，G是BD上一點，連接CG并延長交BA的延長線于點F，交AD于點E，連接AG.
(1)求證：AG＝CG；
(2)求證：AG2＝GE·GF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com