
【題目】如圖,P是正三角形ABC內的一點,且PA=6,PB=8,PC=10,將△APB繞點B逆時針旋轉一定角度后,可得到△CQB. 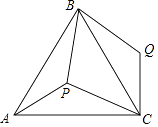
(1)求點P與點Q之間的距離;
(2)求∠APB的度數.
【答案】
(1)解:連接PQ,
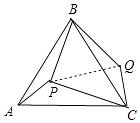
由旋轉性質有:
BQ=BP=8,QC=PA=6,∠QBC=∠ABP,∠BQC=∠BPA,
∴∠QBC+∠PBC=∠ABP+∠PBC
即∠QBP=∠ABC,
∵△ABC是正三角形,
∴∠ABC=60°,
∴∠QBP=60°,
∴△BPQ是正三角形,
∴PQ=BP=BQ=8
(2)解:在△PQC中,PQ=8,QC=6,PC=10
∴PQ2+QC2=PC2,
∴∠PQC=90°,
∴∠APB=∠BQC=∠BQP+∠PQC=60°+90°=150°
【解析】(1)由旋轉的性質可以證明△PBQ是等邊三角形,即可解決問題.(2)利用勾股定理的逆定理證明∠PQC=90°,由∠BQC=∠APB,即可解決問題.
【考點精析】掌握等邊三角形的性質和勾股定理的逆定理是解答本題的根本,需要知道等邊三角形的三個角都相等并且每個角都是60°;如果三角形的三邊長a、b、c有下面關系:a2+b2=c2,那么這個三角形是直角三角形.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:初中數學 來源: 題型:
【題目】近年來,我國逐步完善養老金保險制度,甲、乙兩人計劃用相同的年數分別繳納養老保險金15萬元和10萬元,甲計劃比乙每年多繳納養老保險金0.2萬元.求甲、乙兩人計劃每年分別繳納養老保險金多少萬元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】長城科技公司生產銷售一種電子產品,該產品總成本包括技術成本、制造成本、銷售成本三部分,經核算,2014年該產品各部分成本所占比例約為2:a:1.且2014年該產品的技術成本、制造成本分別為400萬元、1400萬元.
(1)確定a的值,并求2014年產品總成本為多少萬元;
(2)為降低總成本,該公司2015年及2016年增加了技術成本投入,確保這兩年技術成本都比前一年增加一個相同的百分數m(m<50%),制造成本在這兩年里都比前一年減少一個相同的百分數2m;同時為了擴大銷售量,2016年的銷售成本將在2014年的基礎上提高10%,經過以上變革,預計2016年該產品總成本達到2014年該產品總成本的 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,點D、E、F分別是邊AB、AC、BC的中點,要判定四邊形DBFE是菱形,下列所添加條件不正確的是( )

A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目:初中數學 來源: 題型:
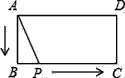
【題目】如圖,矩形ABCD中,AB=2,BC=4,P為矩形邊上的一個動點,運動路線是A→B→C→D→A,設P點經過的路程為x,以A,P,B為頂點的三角形面積為y,則選項圖象能大致反映y與x的函數關系的是( )
A. 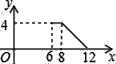 B.
B. 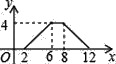 C.
C. 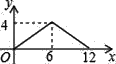 D.
D. 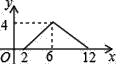
查看答案和解析>>
科目:初中數學 來源: 題型:
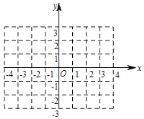
【題目】已知一次函數![]() ,它的圖象與
,它的圖象與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
![]() 點
點![]() 的坐標為________,點
的坐標為________,點![]() 的坐標為________;
的坐標為________;
![]() 畫出此函數圖象;
畫出此函數圖象;
![]() 畫出該函數圖象向下平移
畫出該函數圖象向下平移![]() 個單位長度后得到的圖象;
個單位長度后得到的圖象;
![]() 寫出一次函數
寫出一次函數![]() 圖象向下平移
圖象向下平移![]() 個單位長度后所得圖象對應的表達式.
個單位長度后所得圖象對應的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們規定:平面內點A到圖形G上各個點的距離的最小值稱為該點到這個圖形的最小距離d,點A到圖形G上各個點的距離的最大值稱為該點到這個圖形的最大距離D,定義點A到圖形G的距離跨度為R=D﹣d. 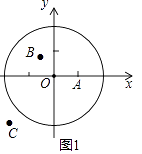
(1)①如圖1,在平面直角坐標系xOy中,圖形G1為以O為圓心,2為半徑的圓,直接寫出以下各點到圖形G1的距離跨度: A(1,0)的距離跨度;
B(﹣ ![]() ,
, ![]() )的距離跨度;
)的距離跨度;
C(﹣3,﹣2)的距離跨度;
②根據①中的結果,猜想到圖形G1的距離跨度為2的所有的點組成的圖形的形狀是 .
(2)如圖2,在平面直角坐標系xOy中,圖形G2為以D(﹣1,0)為圓心,2為半徑的圓,直線y=k(x﹣1)上存在到G2的距離跨度為2的點,求k的取值范圍. 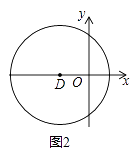
(3)如圖3,在平面直角坐標系xOy中,射線OP:y= ![]() x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,直接寫出圓心E的橫坐標xE的取值范圍 .
x(x≥0),⊙E是以3為半徑的圓,且圓心E在x軸上運動,若射線OP上存在點到⊙E的距離跨度為2,直接寫出圓心E的橫坐標xE的取值范圍 . 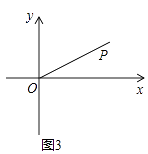
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com