
【題目】如圖1,在正方形ABCD中,E,F,G,H分別為邊AB,BC,CD,DA上的點,HA=EB=FC=GD,連接EG,FH,交點為O.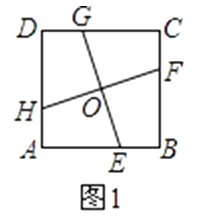
(1)如圖1,連接GH,GF,求證:GH=GF;
(2)如圖2,連接EF,FG,GH,HE,試判斷四邊形EFGH的形狀,并證明你的結論;
(3)將正方形ABCD沿線段EG,HF剪開,再把得到的四個四邊形按圖3的方式拼接成一個四邊形.若正方形ABCD的邊長為3cm,HA=EB=FC=GD=1cm,則圖3中陰影部分的面積為cm2 . (直接寫結果)
【答案】
(1)證明:∵四邊形EFGH是正方形. ∴∠C=∠D=90°,AB=BC=CD=DA, ∵HA=EB=FC=GD,
∴AE=BF=CG=DH, ∴△CGF≌△DHG ∴ GH=GF;
(2)證明:∵四邊形ABCD是正方形,
∴∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,
∵HA=EB=FC=GD,
∴AE=BF=CG=DH,
∴△AEH≌△BFE≌△CGF≌△DHG,
∴EF=FG=GH=HE,
∴四邊形EFGH是菱形,
∵△DHG≌△AEH,
∴∠DHG=∠AEH,
∵∠AEH+∠AHE=90°,
∴∠DHG+∠AHE=90°,
∴∠GHE=90°,
∴四邊形EFGH是正方形
(3)解:S陰影=1. ∵HA=EB=FC=GD=1,AB=BC=CD=AD=3, ∴GF=EF=EH=GH= ![]() ,
,
∵由(1)知,四邊形EFGH是正方形, ∴GO=OF,∠GOF=90°, 由勾股定理得:GO=OF= ![]() ,
,
∵S四邊形FCGO= ![]() ×1×2+
×1×2+ ![]() ×
× ![]() ×
× ![]() =
= ![]() , ∴S陰影=
, ∴S陰影= ![]() ﹣S四邊形FCGO×4=10﹣9=1
﹣S四邊形FCGO×4=10﹣9=1
【解析】(1)根據正方形的性質得出∠C=∠D=90°,AB=BC=CD=DA, 結合已知得出AE=BF=CG=DH,從而判斷出△CGF≌△DHG,根據全等三角形的性質得出結論;
(2)根據正方形的性質得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA, 結合已知得出AE=BF=CG=DH,從而推出△AEH≌△BFE≌△CGF≌△DHG,由全等三角形的性質得出EF=FG=GH=HE,進而判斷出四邊形EFGH是菱形,再找出∠GHE=90°,根據正方形的判定得出四邊形EFGH是正方形;
(3)根據已知條件,知道重新拼出來的圖形是正方形,利用勾股定理求出GF,GO,FO的長,從而求出陰影部分的面積。
【考點精析】掌握勾股定理的概念是解答本題的根本,需要知道直角三角形兩直角邊a、b的平方和等于斜邊c的平方,即;a2+b2=c2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】我國倡導的“一帶一路”建設將促進我國與世界各國的互利合作,“一帶一路”地區覆蓋總人口約為4400000000人,將數據4400000000用科學記數法表示為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式由左到右的變形中,屬于因式分解的是( )
A. a(m+n)= am+an B. a2﹣b2﹣c2 =(a﹣b)(a+b)﹣c2
C. 10x2﹣5x = 5x(2x﹣1) D. x2﹣16+6x =(x+4)(x﹣4)+ 6x
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中任意一點p(x,y)經平移后對應點為p1(x+5,y+3),將△ABC作同樣的平移得到△A1B1C1.
(1)畫出△A1B1C1;
(2)求A1,B1,C1的坐標;
(3)寫出平移的過程.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知E、F分別為平行四邊形ABCD的對邊AD、BC上的點,且DE=BF,EM⊥AC于M,FN⊥AC于N,EF交AC于點O,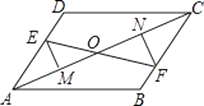
求證:
(1)EM=FN;
(2)EF與MN互相平分.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國人很早開始使用負數,中國古代數學著作《九章算術》的“方程”一章,在世界數學史上首次正式引入負數.如果收入100元記作+100元.那么﹣80元表示( )
A.支出20元
B.收入20元
C.支出80元
D.收入80元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題14分)如圖,點A和動點P在直線![]() 上,點P關于點A的對稱點為Q,以AQ為邊作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圓O。點C在點P右側,PC=4,過點C作直線
上,點P關于點A的對稱點為Q,以AQ為邊作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圓O。點C在點P右側,PC=4,過點C作直線![]() ⊥
⊥![]() ,過點O作OD⊥
,過點O作OD⊥![]() 于點D,交AB右側的圓弧于點E。在射線CD上取點F,使DF=
于點D,交AB右側的圓弧于點E。在射線CD上取點F,使DF=![]() CD,以DE,DF為鄰邊作矩形DEGF,設AQ=
CD,以DE,DF為鄰邊作矩形DEGF,設AQ=![]()
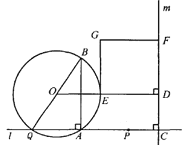
(1)用關于![]() 的代數式表示BQ,DF;
的代數式表示BQ,DF;
(2)當點P在點A右側時,若矩形DEGF的面積等于90,求AP的長;
(3)在點P的整個運動過程中,
①當AP為何值時,矩形DEGF是正方形?
②作直線BG交⊙O于另一點N,若BN的弦心距為1,求AP的長(直接寫出答案)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com